
分析 (1)由直线与圆相切,得到圆心到切线的距离d等于半径r,利用点到直线的距离公式求出圆心M到已知直线的距离d,即为圆M的半径,写出圆M方程即可;
(2)分类讨论,利用圆心到直线的距离等于半径,即可求直线l的方程;
(3)设P(x,y),利用两点间的距离公式化简已知的等式,整理后得到x与y的关系式,再表示出两向量的坐标,利用平面向量的数量积运算法则计算所求的式子,将表示出的关系式代入得到关于y的式子,由P在圆M内部,得到P与圆心M的距离小于半径列出不等式,即可求出所求式子的范围.
解答 解:(1)依题意,圆M的半径r等于圆心M(-1,0)到直线$x-\sqrt{3}y-3=0$的距离,
即$r=\frac{{|{-1-3}|}}{{\sqrt{1+3}}}=2$,∴圆M的方程为(x+1)2+y2=4.
(2)当斜率存在时,设直线方程l:y=kx+3,则圆心到直线的距离$\frac{{|{k-3}|}}{{\sqrt{1+{k^2}}}}=1$,
∴$k=\frac{4}{3}$,直线方程l:4x-3y+9=0
当直线斜率不存在时,则l:x=0,经检验满足条件
综上,直线方程l:4x-3y+9=0或x=0;
(3)设P(x,y),由|PA||PB|=|PO|2,
得$\sqrt{{{({x+2})}^2}+{y^2}}•\sqrt{{{({x-2})}^2}+{y^2}}={x^2}+{y^2}$,即x2-y2=2.
∴$\overrightarrow{PA}•\overrightarrow{PB}=({-2-x,-y})•({2-x,-y})={x^2}-4+{y^2}=2({{y^2}-1})$.
∵点P在圆M内,∴(x+1)2+y2<4,∴0≤y2<4,∴-1≤y2-1<3.
∴$\overrightarrow{PA}•\overrightarrow{PB}$的取值范围为[-2,6).
点评 此题考查了圆的标准方程,涉及的知识有:点到直线的距离公式,两点间的距离公式,以及点与圆、直线与圆的位置关系,熟练掌握公式及法则是解本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
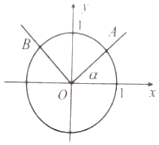 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A(x1,y1),角β=α+$\frac{2π}{3}$的终边与单位圆交于点B(x2,y2),记f(α)=y1-y2.若角α为锐角,则f(α)的取值范围是(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A(x1,y1),角β=α+$\frac{2π}{3}$的终边与单位圆交于点B(x2,y2),记f(α)=y1-y2.若角α为锐角,则f(α)的取值范围是(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com