
分析 (1)根据函数f(x)是奇函数,求出a=0即可;
(2)根据函数g(x)在(-2,+∞)上单调递减,得到g(x1)-g(x2)>0,从而求出m的范围即可;
(3)问题转化为x=0或 mx2+x+m+2=0,通过讨论m的范围结合二次函数的性质求出m的范围即可.
解答 解:(1)∵函数f(x)是奇函数,∴f(-x)=-f(x),
∴$\frac{-x+a}{{x}^{2}+1}$=-$\frac{x+a}{{x}^{2}+1}$,得a=0…(2分)
(2)∵$g(x)=\frac{mx}{2+x}$在(-2,+∞)上单调递减,
∴任给实数x1,x2,当-2<x1<x2时,g(x1)>g(x2),
∴$g({x_1})-g({x_2})=\frac{{m{x_1}}}{{2+{x_1}}}-\frac{{m{x_2}}}{{2+{x_2}}}=\frac{{2m({x_1}-{x_2})}}{{(2+{x_1})(2+{x_2})}}>0$
∴m<0…(5分)
(3)由(1)得f(x)=$\frac{x}{{x}^{2}+1}$,令h(x)=0,即$\frac{x}{{{x^2}+1}}+\frac{mx}{2+x}=0$.
化简得x(mx2+x+m+2)=0.
∴x=0或 mx2+x+m+2=0…(7分)
若0是方程mx2+x+m+2=0的根,则m=-2,
此时方程mx2+x+m+2=0的另一根为$\frac{1}{2}$,符合题意…(8分)
若0不是方程mx2+x+m+2=0的根,
则函数h(x)=f(x)+g(x)在区间(-1,1)上有且仅有两个不同的零点
等价于方程mx2+x+m+2=0(※)在区间(-1,1)上有且仅有一个非零的实根…(9分)
①当△=12-4m(m+2)=0时,得$m=\frac{{-2±\sqrt{5}}}{2}$.
若$m=\frac{{-2-\sqrt{5}}}{2}$,则方程(※)的根为$x=-\frac{1}{2m}=-\frac{1}{{-2-\sqrt{5}}}=\sqrt{5}-2∈({-1,\;1})$,符合题意;
若$m=\frac{{-2+\sqrt{5}}}{2}$,则与(2)条件下m<0矛盾,不符合题意.
∴$m=\frac{{-2-\sqrt{5}}}{2}$…(10分)
③当△>0时,令ω(x)=mx2+x+m+2
由$\left\{\begin{array}{l}{ω(-1)•ω(1)<0}\\{ω(0)≠0}\end{array}\right.$,得$\left\{\begin{array}{l}(2m+1)(2m+3)<0\\ m+2≠0\end{array}\right.$,
解得$-\frac{3}{2}<m<-\frac{1}{2}$…(12分)
综上所述,所求实数m的取值范围是$({-\frac{3}{2},\;-\frac{1}{2}})∪\left\{{-2,\frac{{-2-\sqrt{5}}}{2}}\right\}$…(13分)
点评 本题考查了函数的单调性、奇偶性问题,考查二次函数的性质以及分类讨论思想,是一道中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{5}{4}$,$\frac{5}{3}$] | B. | [$\frac{3}{2}$,++∞) | C. | (1,4] | D. | [$\frac{3}{2}$,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,6] | B. | [-3,3]∪[5,+∞) | C. | $[{-6,4+\sqrt{6}}]$ | D. | $[{-6,6}]∪[{4+\sqrt{6},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
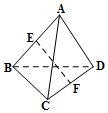 空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=$\sqrt{3}$,则异面直线AD,BC所成的角的补角为( )
空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=$\sqrt{3}$,则异面直线AD,BC所成的角的补角为( )| A. | 120° | B. | 60° | C. | 90° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {1,2} | C. | {0,3} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $±\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$且2 | D. | $\frac{1}{2}$或2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com