
| ���� | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
| �Żݽ��x��ǧԪ�� | 10 | 11 | 13 | 12 | 8 |
| ������y������ | 23 | 25 | 30 | 26 | 16 |
���� ��1�����ݱ������ݼ���$\overline{x}$��$\overline{y}$������ع�ϵ����д�����Իع鷽�̣�
��2���ɣ�1�������Իع鷽�����x=10ʱ��x=8ʱy��ֵ���Ƚ����ɣ�
��� �⣺��1�����ݱ������ݣ�����$\overline{x}$=$\frac{1}{3}$����11+13+12��=12��
$\overline{y}$=$\frac{1}{3}$����25+30+26��=27��
$\sum_{i=1}^{3}$xiyi=��11��25+13��30+12��26��=977��
$\sum_{i=1}^{3}$${{x}_{i}}^{2}$=112+132+262=434��
��$\hat b=\frac{{\sum_{i=1}^3{{x_i}{y_i}-3\overline x•\overline y}}}{{\sum_{i=1}^3{x_i^2-3{{\overline x}^2}}}}$=$\frac{977-3��12��27}{{434-3��{{12}^2}}}=2.5$��
$\hat a=\overline y-\hat b\overline x$=27-2.5��12=-3��
�����Իع鷽����$\hat y=2.5x-3$��
��2���ɣ�1��֪����x=10ʱ��y=2.5��10-3=22��������2����
��x=8ʱ��y=2.5��8-3=17��������2����
������õ����Իع鷽���ǿɿ��ģ�
���� ���⿼�������Իع鷽�̵�����Ӧ�����⣬�ǻ����⣮


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��6 | B�� | 3��6 | C�� | 3��7 | D�� | 1��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �������������У���������ֱ�������ε�ֱ��������Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ������ͼ������ƽ�־��ε��������á�ǵ�¡����������Ϊ$\frac{8\sqrt{2}��}{3}$��
�������������У���������ֱ�������ε�ֱ��������Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ������ͼ������ƽ�־��ε��������á�ǵ�¡����������Ϊ$\frac{8\sqrt{2}��}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
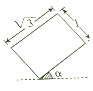 һ��������ˮƽ�����ϵ����������ĸ���ͼ��ͼ��ʾ�����Ц�Ϊ��ǣ���ü����������ͼ����������ֵΪ��������
һ��������ˮƽ�����ϵ����������ĸ���ͼ��ͼ��ʾ�����Ц�Ϊ��ǣ���ü����������ͼ����������ֵΪ��������| A�� | 2��3 | B�� | 2$\sqrt{3}$��3 | C�� | 1��3 | D�� | 2��2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 8+8�� | B�� | 8+6�� | C�� | 6+8�� | D�� | 6+6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
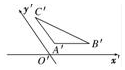 ��ͼ��������ABC��ֱ��ͼ����ABCƽ��ͼ����ֱ�������Σ����������Ρ���������Ρ��۽������Ρ�ֱ�������λ��ߵ��������Σ�
��ͼ��������ABC��ֱ��ͼ����ABCƽ��ͼ����ֱ�������Σ����������Ρ���������Ρ��۽������Ρ�ֱ�������λ��ߵ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com