Question

20．如图，已知多面体ABCDFEF中，平面ADEF⊥平面ABCD，若四边形ADEF为矩形，AB∥CD，$AB=\frac{1}{2}CD$，BC⊥BD，M为EC中点．
（1）求证：BC⊥平面BDE；
（2）求证：BM∥平面ADEF．

Answer 1

分析 （1）只要证明DE⊥平面ABCD即可；
（2）取DE中点N，连接AN，MN，只要证明BM∥AN，利用线面平行的判定定理可得．

解答 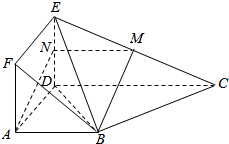证明：（1）因为四边形ADEF为矩形，所以DE⊥AD，…（1分）
又因为平面ADEF⊥平面ABCD，
平面ADEF∩平面ABCD=AD，
所以DE⊥平面ABCD，…（3分）
又因为BC?平面ABCD，
所以DE⊥BC，…（5分）
又因为BC⊥BD，DE∩BD=D，所以BC⊥平面BDE； …（7分）
（2）取DE中点N，连接AN，MN，因为M，N分别为EC，DE中点，
所以MN∥CD，$MN=\frac{1}{2}CD$，…（9分）
又因为AB∥CD，$AB=\frac{1}{2}CD$，所以MN∥AB，MN=AB，
所以四边形ABMN为平行四边形，…（11分）
所以BM∥AN，又AN?平面ADEF，BM?平面ADEF，
所以BM∥平面ADEF．…（14分）

点评 本题考查了线面垂直、线面平行的判定定理和判定定理的运用；关键是熟练掌握定理性质．