
自驾游从A地到B地有甲乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表所示.
| | CD段 | EF段 | GH段 |
| 堵车概率 | 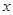 | 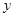 | 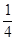 |
| 平均堵车时间 (单位:小时) |  | 2 | 1 |
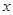 在
在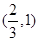 上变化,
上变化,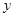 在
在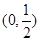 上变化.
上变化.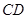 段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1, 2] | 6 |
| (2, 3] | 38 |
| (3, 4] | 24 |
| (4, 5] | 24 |
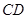 段平均堵车时间
段平均堵车时间 的值;
的值;(1)3;(2)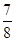 .
.
解析试题分析:本题考查利用频率分布表求平均数,相互独立事件同时发生的概率,离散型随机变量分布列,数学期望,几何概型等基础知识;考查运用统计、概率、数学期望等数学知识解决实际问题的能力,以及运算求解能力;考查数形结合数学思想方法.第一问,用总的堵车时间除以总人数100人,即得到平均堵车时间;第二问,利用独立事件求出每种情况的概率,选择甲路线说明甲需汽油费少,利用线性规划化画出区域图,再利用几何概型求概率;法二,分别求EF路段和GH路段的期望再相加求乙路线多花汽油费的期望.
试题解析:(1)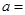
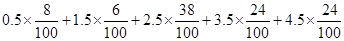 2分
2分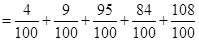
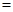 3. 4分
3. 4分
(2)设走甲线路所花汽油费为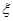 元,
元,
则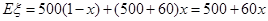 . 5分
. 5分
法一:设走乙线路多花的汽油费为 元,∵
元,∵ 段与
段与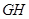 段堵车与否相互独立,
段堵车与否相互独立,
∴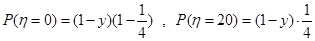 ,
,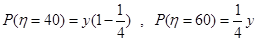 , 7分
, 7分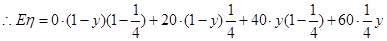
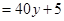 . 8分
. 8分
∴走乙线路所花的汽油费的数学期望为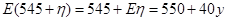 . 9分
. 9分
依题意,选择走甲线路应满足 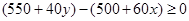 , 10分
, 10分
即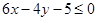 ,又
,又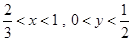 ,
,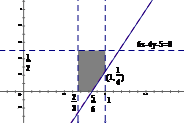
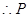 (选择走甲线路)
(选择走甲线路)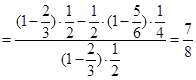 . 13分
. 13分
法二:在EF路段多花汽油费的数学期望是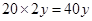 元, 6分
元, 6分
在GH路段多花汽油费的数学期望是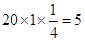 元, 7分
元, 7分
因为EF、GH路段堵车与否相互独立,
所以走乙路线多花汽油费的数学期望是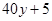 元. 8分
元. 8分
以下解法同法一.
考点:利用频率分布表求平均数,相互独立事件同时发生的概率,离散型随机变量分布列,数学期望,几何概型.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
袋中装有编号为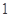 的球
的球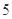 个,编号为
个,编号为 的球
的球 个,这些球的大小完全一样。
个,这些球的大小完全一样。
(1)从中任意取出四个,求剩下的四个球都是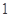 号球的概率;
号球的概率;
(2)从中任意取出三个,记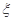 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量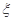 的分布列及其数学期望
的分布列及其数学期望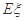 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
同时抛掷4枚均匀的硬币80次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为 .
.
(1)求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
(2)求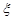 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂在试验阶段大量生产一种零件,这种零件有 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为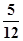 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为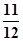 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽取该种零件 个,设
个,设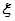 表示其中合格品的个数,求
表示其中合格品的个数,求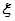 的分布列及数学期望
的分布列及数学期望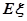 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
 .(12分)
.(12分) ,求
,求 的分布列与期望.
的分布列与期望. | 0.15 | 0.10 | 0.05[ | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对每道甲类题的概率都是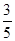 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是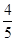 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用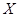 表示张同学答对题的个数,求
表示张同学答对题的个数,求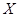 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某电视台的一个智力游戏节目中,有一道将中国四大名著《三国演义》、《水浒传》、《西游记》、《红楼梦》与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线,每连对一个得2分,连错得-1分,某观众只知道《三国演义》的作者是罗贯中,其他不知道随意连线,将他的得分记作ξ.
(1)求该观众得分ξ为负数的概率;
(2)求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一盒中共装有除颜色外其余均相同的小球12个,其中5个红球、4个黑球、2个白球、1个绿球.从中随机取出1个球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com