解:(1)由f(1)=0,导函数
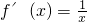
可知f(x)=lnx,x>0,
∵g(x)=f(x)+f'(x),∴
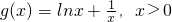
.
求导函数可得

,
所以当x∈(0,1)时,g'(x)<0;x∈(1,+∞)时,g'(x)>0,
故函数的单调增区间为(1,+∞),单调减区间为(0,1),极小值为g(1)=1
∵函数在定义域上仅有一个极小值,∴也为最小值,最小值为g(1)=1.
(2)设
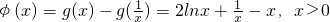
,则
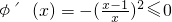
,故函数在定义域内为减函数,
∵φ(1)=0,
∴当x∈(0,1)时,φ(x)>0,即g(x)>

;x∈(1,+∞)时,φ(x)<0,即g(x)<

;x=1时,g(x)=

.
(3)假设存在满足题设的x
0,则
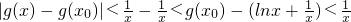
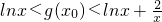
,对任意x>0成立,
从而有

∵lnx→+∞,
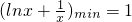
∴无解,故不存在.
分析:(1)根据题意求出f(x)的解析式,代入g(x)=f(x)+f′(x).求出g(x),求导,根据导数的正负取得函数的单调区间,从而可得函数的最小值;
(2)构造函数φ(x),利用导数求该函数的最小值,从而求得g(x)与

的大小大小关系;
(3)假设存在x
0>0,使得
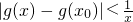
对任意x>0成立,转化为封闭型命题,利用研究函数的最值可得结论.
点评:本题考查利用导数研究函数的单调性和在闭区间上的最值问题,考查分类讨论的思想方法.其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

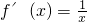 ,g(x)=f(x)+f'(x).
,g(x)=f(x)+f'(x). 的大小关系;
的大小关系;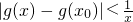 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.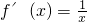 可知f(x)=lnx,x>0,
可知f(x)=lnx,x>0,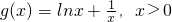 .
. ,
,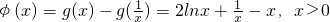 ,则
,则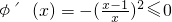 ,故函数在定义域内为减函数,
,故函数在定义域内为减函数, ;x∈(1,+∞)时,φ(x)<0,即g(x)<
;x∈(1,+∞)时,φ(x)<0,即g(x)< ;x=1时,g(x)=
;x=1时,g(x)= .
.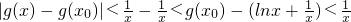
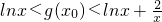 ,对任意x>0成立,
,对任意x>0成立,
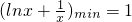
 的大小大小关系;
的大小大小关系;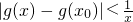 对任意x>0成立,转化为封闭型命题,利用研究函数的最值可得结论.
对任意x>0成立,转化为封闭型命题,利用研究函数的最值可得结论.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案