练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求函数f(x)=x2+2ax-1在区间［0,3］上的最小值.

    思路解析:讨论函数f(x)=x2+2ax-1在区间［0,3］上的单调性,即可确定函数在区间［0,3］上的最小值.

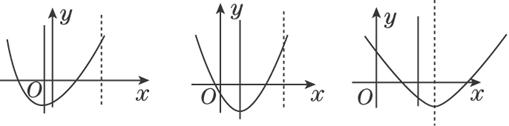
    解:抛物线开口向上,对称轴是x=-a.当x=-a≤0即a≥0时,函数f(x)在区间［0,3］上是单调递增的,∴f(x) min=f(0)=-1.

    当0＜-a≤3,即-3≤a＜0时,函数f(x)在区间［0,3］上是先单调递减再单调递增的,∴f(x) min=f(-a)=-a2-1.

    当-a＞3即a＜-3时,函数f(x)在区间［0,3］上是单调递减的,∴f(x) min=f(-3)=8+6a.

    深化升华

    求函数在某闭区间上的最值的问题,实质上是研究函数在该闭区间上的单调性,利用函数在该区间上的单调性判断函数在什么位置取到最值(或区间端点,或区间上某点),从而可以求函数在该闭区间上的单调性.此外,对于有参变量的函数需要注意的是参数对函数图象的影响,并恰当地进行分类讨论.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    求函数f(x)=
    		x2+x
    (x≤-1)    的反函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求函数f(x)=
    		x2-2x+2
    +
    		x2-4x+8
    的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）已知函数f(x)=
    (x+1)0
    		|x|-x
    ，求f（-2）的值和函数的定义域
    （2）求函数f(x)=
    		-x2-2x+3
    的定义域和值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）求函数f(x)=
    		x2-5x+6
    +
    (x-1)0
    		x+|x|
    的定义域．
    （2）求函数y=
    x2-x
    x2-x+1
    的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对定义在实数集R上的函数f1（x），f2（x），令F（x）=f1（x）+f2（x），已知对任意不同的实数x1，x2，|f1（x1）-f1（x2）|＞|f2（x1）-f2（x2）|．
    （1）若y=f1（x）是区间D上的增函数，能否确定y=F（x）是区间D上的增函数？若能够确定，说明理由；若不能，请举例说明；
    （2）若y=f2（x）是区间D上的增函数，能否确定y=F（x）是区间D上的增函数？若能够确定，说明理由；若不能，请举例说明；
    （3）求函数f(x)=x2+
    14x
    (x＞0)    的单调区间．

    查看答案和解析>>

    同步练习册答案