
【题目】设数列 ![]() 的前n项和为Sn
的前n项和为Sn ![]() ,且满足:
,且满足:
① ![]() ;②
;② ![]() ,其中
,其中 ![]() 且
且 ![]() .
.
(1)求p的值;
(2)数列 ![]() 能否是等比数列?请说明理由;
能否是等比数列?请说明理由;
(3)求证:当r ![]() 2时,数列
2时,数列 ![]() 是等差数列.
是等差数列.
【答案】
(1)
解:(1)n ![]() 1时,
1时, ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,
,
又 ![]() ,所以p
,所以p ![]() 1.
1.
(2)![]()
不是等比数列.理由如下:
假设 ![]() 是等比数列,公比为q,
是等比数列,公比为q,
当n ![]() 2时,
2时, ![]() ,即
,即 ![]() ,
,
所以 ![]() (i)
(i)
当n ![]() 3时,
3时, ![]() ,即
,即 ![]() ,
,
所以 ![]() , (ii)
, (ii)
由(i)(ii)得q ![]() 1,与
1,与 ![]() 矛盾,所以假设不成立.
矛盾,所以假设不成立.
故 ![]() 不是等比数列.
不是等比数列.
(3)
当r ![]() 2时,易知
2时,易知 ![]() .
.
由 ![]() ,得
,得
![]() 时,
时, ![]() , ①
, ①
![]() ,②
,②
②-①得, ![]() ,
,
即 ![]() ,
,
![]() ,
,
即 ![]()
![]()
![]() ……
……
![]() ,
,
所以 ![]()
令 ![]() d,则
d,则 ![]()
![]() .
.
所以 ![]() .
.
又 ![]() 时,也适合上式,
时,也适合上式,
所以 ![]() .
.
所以 ![]() .
.
所以当r ![]() 2时,数列
2时,数列 ![]() 是等差数列.
是等差数列.
【解析】(1.)将n=1代入②得 ![]() 分析可知只能是
分析可知只能是 ![]() =0,可算出p
=0,可算出p
(2.)假设是等比数列,将n=2、3分别代入得到q,判断是否与已知条件矛盾.
(3.)当n=2时,用前 ![]() 项和减去
项和减去 ![]() 项和可得
项和可得 ![]() 之间关系,分析判断可证
之间关系,分析判断可证 ![]() 是等差数列.
是等差数列.
【考点精析】利用数列的通项公式对题目进行判断即可得到答案,需要熟知如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )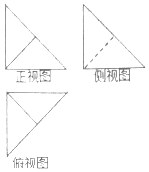
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.若p:?x∈R,x2﹣x+1≥0,则¬p:?x∈R,x2﹣x+1<0
B.“ ![]() ”是“θ=30°或θ=150°”的充分不必要条件
”是“θ=30°或θ=150°”的充分不必要条件
C.命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”
D.已知p:?x∈R,cosx=1,q:?x∈R,x2﹣x+2>0,则“p∧(¬q)”为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.
(Ⅰ)证明:SD⊥平面SAB;
(Ⅱ)求AB与平面SBC所成的角的大小.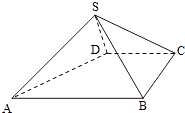
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象在点(x0 , f(x0))处的切线方程l:y=g(x),若函数f(x)满足x∈I(其中I为函数f(x)的定义域),当x≠x0时,[f(x)﹣g(x)](x﹣x0)>0恒成立,则称x0为函数f(x)的“穿越点”.已知函数f(x)=lnx﹣ ![]() x2﹣
x2﹣ ![]() 在(0,e]上存在一个“穿越点”,则a的取值范围为( )
在(0,e]上存在一个“穿越点”,则a的取值范围为( )
A.[ ![]() ,+∞)??
,+∞)??
B.(﹣1, ![]() ]??
]??
C.[﹣ ![]() ,1)??
,1)??
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e1﹣x(﹣a+cosx),a∈R.
(Ⅰ)若函数y=f(x)在[0,π]存在单调增区间,求实数a的取值范围;
(Ⅱ)若f( ![]() )=0,证明:对于x∈[﹣1,
)=0,证明:对于x∈[﹣1, ![]() ],总有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
],总有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=1,E,F分别是CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点. 
(1)证明:AB⊥AC;
(2)证明:DF⊥AE;
(3)是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ![]() ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com