
分析 (1)化根式为分数指数幂,然后利用有理指数幂的运算性质化简求值;
(2)化负指数为正指数,化0指数幂为1,再由有理指数幂的运算性质得答案.
解答 解:(1)$\frac{\sqrt{{a}^{3}{b}^{2}\root{3}{a{b}^{2}}}}{({a}^{\frac{1}{4}}{b}^{\frac{1}{2}})^{4}{a}^{-\frac{1}{3}}{b}^{\frac{1}{3}}}$=$\frac{({a}^{3}{b}^{2}{a}^{\frac{1}{3}}{b}^{\frac{2}{3}})^{\frac{1}{2}}}{a{b}^{2}{a}^{-\frac{1}{3}}{b}^{\frac{1}{3}}}$=${a}^{\frac{3}{2}+\frac{1}{6}-1+\frac{1}{3}}{b}^{1+\frac{1}{3}-2-\frac{1}{3}}$=$\frac{a}{b}$;
(2)(-$\frac{27}{8}$)${\;}^{-\frac{2}{3}}$+(0.002)${\;}^{-\frac{1}{2}}$-10($\sqrt{5}$-2)-1+($\sqrt{2}$-$\sqrt{3}$)0
=$(-\frac{27}{8})^{-\frac{2}{3}}+(\frac{1}{500})^{-\frac{1}{2}}$-$\frac{10}{\sqrt{5}-2}$+1
=$(-\frac{8}{27})^{\frac{2}{3}}+50{0}^{\frac{1}{2}}$-10($\sqrt{5}$+2)+1
=$\frac{4}{9}$+10$\sqrt{5}$-10$\sqrt{5}$-20+1=-$\frac{167}{9}$.
点评 本题考查有理指数幂的化简与求值,是基础的计算题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log2x | B. | ($\frac{1}{2}$)x | C. | $lo{g}_{\frac{1}{2}}x$ | D. | 2x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 16 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
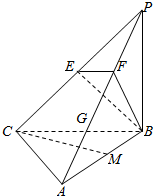 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点G,F是PA上的三等分点.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点G,F是PA上的三等分点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com