
分析 根据当x∈[0,1]时,f(x)=x2-m(x-1)+1(m>0),确定f(x)的对称轴为$x=\frac{m}{2}$,根据对称轴与区间的位置关系进行分类讨论,分别求出f(x)在[0,1]和[0,2]上的值域,列出不等式组,求解即可得到m的取值范围.
解答 解:∵f(1+x)•f(1-x)=4对定义域中的每一个x都成立,
∴f(x+1)=$\frac{4}{f(1-x)}$,
即f(x)=$\frac{4}{f(2-x)}$,
∴当x∈[1,2]时,f(x)=$\frac{4}{f(2-x)}$,其中2-x∈[0,1],
又∵x∈[0,1]时f(x)=x2+m(1-x)+1=x2-mx+m+1,其对称轴方程为$x=\frac{m}{2}$,
①当$\frac{m}{2}>1$,即m>2时,f(x)在[0,1]上的值域为[f(1),f(0)],即[2,m+1],
∴f(x)在[0,2]上的值域为$[2,m+1]∪[\frac{4}{m+1},2]=[\frac{4}{m+1},m+1]$,
由题意,得$\left\{{\begin{array}{l}{m+1≤4}\\{\frac{4}{m+1}≥1}\end{array}}\right.$,∴2<m≤3;
②当$\frac{1}{2}≤\frac{m}{2}≤1$,即1≤m≤2时,f(x)的值域为[f($\frac{m}{2}$),f(0)],即$[m+1-\frac{m^2}{4},m+1]$,
∴f(x)在[0,2]上的值域为$[m+1-\frac{m^2}{4},m+1]∪[\frac{4}{m+1},\frac{4}{{m+1-\frac{m^2}{4}}}]$,
由题意,得$\left\{{\begin{array}{l}{\frac{4}{{m+1-\frac{m^2}{4}}}≤4}\\{m+1≤4}\end{array}}\right.$,且$\left\{{\begin{array}{l}{m+1-\frac{m^2}{4}≥1}\\{\frac{4}{m+1}≥1}\end{array}}\right.$,解得1≤m≤2;
③当$0<\frac{m}{2}≤\frac{1}{2}$,即0<m≤1时,f(x)的值域为[f($\frac{m}{2}$),f(1)],即$[m+1-\frac{m^2}{4},2]$,
∴f(x)在[0,2]上的值域为$[m+1-\frac{m^2}{4},2]∪[2,\frac{4}{{m+1-\frac{m^2}{4}}}]$,即$[m+1-\frac{m^2}{4},\frac{4}{{m+1-\frac{m^2}{4}}}]$,
由题意,得$\left\{{\begin{array}{l}{m+1-\frac{m^2}{4}≥1}\\{\frac{4}{{m+1-\frac{m^2}{4}}}≤4}\end{array}}\right.$,解得0<m≤1.
综合①②③,所求m的取值范围是0<m≤3.
故答案为:0<m≤3
点评 本题主要考查函数与方程的应用,根据条件转化为一元二次函数,结合函数单调性和值域之间的关系是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 产品A | 8 | 12 | 40 | 32 | 8 |
| 产品B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
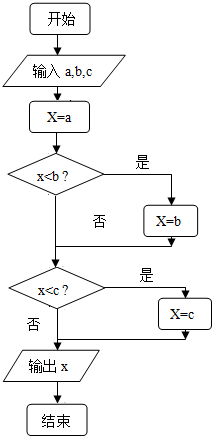
| A. | 0.25 | B. | 0.5 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com