
分析 设出原点为顶点的抛物线方程可设为x2=py(p≠0)或y2=qx(q≠0),得到$\frac{9}{p}$=($\frac{c}{4}$)n-2对n∈N*恒成立或3q=($\frac{c}{\sqrt{2}}$)n-2对n∈N*恒成立,求出c的值即可.
解答 解:记函数f(x)=cn-2(1-|$\frac{x}{{2}^{n-2}}$-3|),(2n-1≤x≤2n,n∈N*)的极大值点为pn(xn,yn).
以原点为顶点的抛物线方程可设为x2=py(p≠0)或y2=qx(q≠0).
若pn(3•2n-2,cn-2).在抛物线x2=py(p≠0)上,则(3•2n-2)2=pcn-2,
即$\frac{9}{p}$=($\frac{c}{4}$)n-2对n∈N*恒成立,从而c=4,p=9,抛物线方程为x2=9y;
若pn(3•2n-2,cn-2).在抛物线y2=qx(q≠0)上,则(cn-2)2=3q•2n-2,
即3q=($\frac{c}{\sqrt{2}}$)n-2对n∈N*恒成立,从而c=$\sqrt{2}$,q=$\frac{1}{3}$,抛物线方程为y2=$\frac{1}{3}$x,
综上:c=4或$\sqrt{2}$,
故答案为:4或$\sqrt{2}$.
点评 本小题主要考查抛物线的标准方程、利用导数研究函数的极值、不等式的解法,考查运算求解能力、化归与转化思想,是一道中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
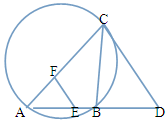 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα=$\frac{3}{5}$ | B. | cosα=-$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | tanα=-$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
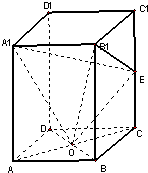 长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.
长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com