
分析 (Ⅰ)求出圆的半径,即可求圆C的方程;
(Ⅱ)已知点P是圆C上的动点,求出圆心到直线l的距离,即可求点P到直线$\sqrt{3}$x+y-6=0的距离的最小值;
(Ⅲ)利用C点到直线l的距离等于圆的半径2,求出b,k的关系,表示出三角形的面积,利用基本不等式,即可求△ABC的面积最小时直线L的方程.
解答 解:(Ⅰ)圆C的半径为$|CM|=\sqrt{1+3}=2$,…(1分)
所以圆C的方程为x2+y2=4…(2分)
(Ⅱ)圆心到直线l的距离为$d=\frac{|-6|}{{\sqrt{3+1}}}=3$,…(4分)
所以P到直线l:x+y-4=0的距离的最小值为1 …(6分)
(Ⅲ)设直线l的方程为:y=kx+b,因为l与x,y轴的正半轴分别相交于A,B两点,
则k<0,b>0,且$A(-\frac{b}{k}\;,\;0)\;,\;\;B(0\;,\;b)$,…(7分)
又l与圆C相切,则C点到直线l的距离等于圆的半径2,
即:$\frac{|b|}{{\sqrt{{k^2}+1}}}=2⇒{b^2}=4{k^2}+4$,①,…(8分)
而${S_{△ABC}}=\frac{1}{2}(-\frac{b}{k})b=\frac{{-{b^2}}}{2k}$②…(9分)
将①代入②得${S_{△ABC}}=\frac{{-(4{k^2}+4)}}{2k}=2(-k+\frac{1}{-k})≥4\sqrt{(-k)•\frac{1}{-k}}=4$,当且仅当k=-1时取等号,所以当k=-1时,△ABC的面积最小,此时${b^2}=4{k^2}+4=8,\;\;\;\;b=2\sqrt{2}$,…(11分)
直线l的方程为:$y=-x+2\sqrt{2}$…(12分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查三角形面积的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
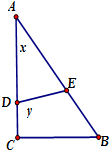 如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.
如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{3}{8}$ | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com