
分析 (1)求出函数的导数,列出表格求出函数的极值即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的零点个数即可.
解答 解:(1)$f'(x)=a{x^2}-(a+1)x+1=a(x-1)(x-\frac{1}{a})$,
∵a<0,∴$\frac{1}{a}<1$
| $(-∞,\frac{1}{a})$ | $\frac{1}{a}$ | $(\frac{1}{a},1)$ | 1 | (1,+∞) | |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
点评 本题考查了求函数的单调性、极值问题,考查导数的应用以及函数的零点问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
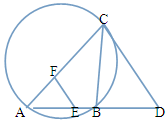 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log0.7 6<0.7 6<6 0.7 | B. | 0.7 6<6 0.7<log0.7 6 | ||
| C. | log0.7 6<6 0.7<0.76 | D. | 0.7 6<log0.7 6<6 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
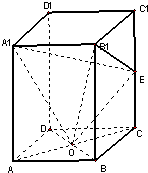 长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.
长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com