
【题目】如图,四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() .
.
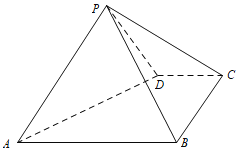
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
1)推导出![]() ,从而
,从而![]() ,设
,设![]() 为
为![]() 边的中点,连结
边的中点,连结![]() ,
,![]() ,推导出四边形
,推导出四边形![]() 为平行四边形,从而
为平行四边形,从而![]() ,进而是
,进而是![]() ,
,![]() 面
面![]() ,由此能证明
,由此能证明![]() .
.
(2)推导出面![]() 面
面![]() ,作
,作![]() 于点
于点![]() ,
,![]() 平面
平面![]() ,以
,以![]() 为原点,
为原点,![]() 方向为
方向为![]() 轴,
轴,![]() 方向为
方向为![]() 轴,
轴,![]() 方向为
方向为![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(1)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,面
,面![]() 面
面![]() ,
,
![]() ,
,![]()
设![]() 为
为![]() 边的中点,连结
边的中点,连结![]() ,
,![]() ,
,
![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
又![]() 为等边三角形,
为等边三角形,![]() ,
,
![]() ,
,![]() 面
面![]()
![]() 面
面![]() ,
,
![]() .
.
(2)![]() 面
面![]() ,
,![]() 平面
平面![]() ,
,![]() 面
面![]() 面
面![]() ,
,
在面![]() 中,作
中,作![]() 于点
于点![]() ,
,![]() 平面
平面![]() ,
,
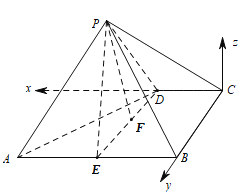
以![]() 为原点,
为原点,![]() 方向为
方向为![]() 轴,
轴,![]() 方向为
方向为![]() 轴,
轴,![]() 方向为
方向为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
如图所示.则![]() ,2,
,2,![]() ,
,![]() ,2,
,2,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则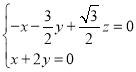 ,
,
取![]() ,得
,得![]() ,
,
![]() 为平面
为平面![]() 的法向量,
的法向量,
则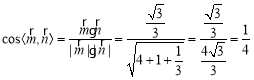 .
.
![]() 二面角
二面角![]() 为锐角,
为锐角,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .三棱锥
.三棱锥![]() 的各个顶点都在球
的各个顶点都在球![]() 表面上,过点
表面上,过点![]() 作球
作球![]() 的截面,若所得截面圆的面积的最大值与最小值之差为
的截面,若所得截面圆的面积的最大值与最小值之差为![]() ,则球
,则球![]() 的表面积为( )
的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2.若
两两垂直,长度分别为1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
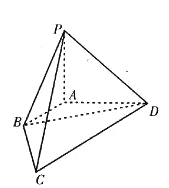
(1)求![]() 的值;
的值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,且
,且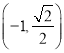 在椭圆E上.
在椭圆E上.
(1)求椭圆E的标准方程;
(2)已知垂直于x轴的直线![]() 交E于A、B两点,垂直于y轴的直线
交E于A、B两点,垂直于y轴的直线![]() 交E于C、D两点,
交E于C、D两点,![]() 与
与![]() 的交点为P,且
的交点为P,且![]() ,间:是否存在两定点M,N,使得
,间:是否存在两定点M,N,使得![]() 为定值?若存在,求出M,N的坐标,若不存在,请说明理由.
为定值?若存在,求出M,N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《宋人扑枣图轴》是作于宋朝的中国古画,现收藏于中国台北故宫博物院.该作品简介:院角的枣树结实累累,小孩群来攀扯,枝桠不停晃动,粒粒枣子摇落满地,有的牵起衣角,有的捧着盘子拾取,又玩又吃,一片兴高采烈之情,跃然于绢素之上.甲、乙、丙、丁四人想根据该图编排一个舞蹈,舞蹈中他们要模仿该图中小孩扑枣的爬、扶、捡、顶四个动作,四人每人模仿一个动作.若他们采用抽签的方式来决定谁模仿哪个动作,则甲不模仿“爬”且乙不模仿“扶”的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,写出直线
的极坐标方程化为直角坐标方程,写出直线![]() 的参数方程的标准形式;
的参数方程的标准形式;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右顶点为
的左、右顶点为![]() ,
,![]() ,上、下顶点为
,上、下顶点为![]() ,
,![]() ,记四边形
,记四边形![]() 的内切圆为
的内切圆为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() 的一条不与坐标轴平行的切线
的一条不与坐标轴平行的切线![]() 交椭圆
交椭圆![]() 于P,M两点.
于P,M两点.
(i)求证:![]() ;
;
(ii)试探究![]() 是否为定值.
是否为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上且
上且![]() .
.
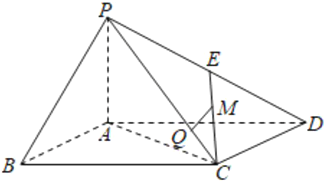
(1)证明![]() 平面
平面![]() ;
;
(2)当![]() 为多大时,在线段
为多大时,在线段![]() 上存在点
上存在点![]() 使得
使得![]() 平面
平面![]() 且
且![]() 与平面
与平面![]() 所成角为
所成角为![]() 同时成立?
同时成立?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com