
【题目】在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .三棱锥
.三棱锥![]() 的各个顶点都在球
的各个顶点都在球![]() 表面上,过点
表面上,过点![]() 作球
作球![]() 的截面,若所得截面圆的面积的最大值与最小值之差为
的截面,若所得截面圆的面积的最大值与最小值之差为![]() ,则球
,则球![]() 的表面积为( )
的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() y2=1(m>1)的离心率为
y2=1(m>1)的离心率为![]() ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面PCD,底面ABCD为梯形,
平面PCD,底面ABCD为梯形,![]() ,
,![]() ,M为PD的中点,过A,B,M的平面与PC交于N.
,M为PD的中点,过A,B,M的平面与PC交于N.![]() ,
,![]() ,
,![]() ,
,![]() .
.
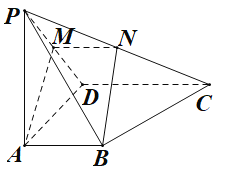
(1)求证:N为PC中点;
(2)求证:![]() 平面PCD;
平面PCD;
(3)T为PB中点,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校开设了素描摄影剪纸书法四门选修课,要求每位同学都要选择其中的两门课程.已知甲同学选了素描,乙与甲没有相同的课程,丙与甲恰有一门课程相同,丁与丙没有相同课程.则以下说法错误的是( )
A.丙有可能没有选素描B.丁有可能没有选素描
C.乙丁可能两门课都相同D.这四个人里恰有2个人选素描
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,
,![]() .
.
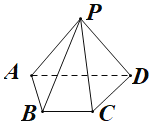
(1)在线段PA上找一点E,使得![]() 平面PCD,并证明;
平面PCD,并证明;
(2)在(1)的条件下,若![]() ,求点E到平面PCD的距离.
,求点E到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 组,得到如图所示的频率分布直方图.若尺寸落在区间
组,得到如图所示的频率分布直方图.若尺寸落在区间![]() 之外,则认为该零件属“不合格”的零件,其中
之外,则认为该零件属“不合格”的零件,其中![]() ,
,![]() 分别为样本平均和样本标准差,计算可得
分别为样本平均和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
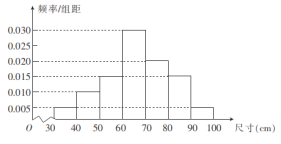
(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前![]() 组中抽出
组中抽出![]() 个零件,标上记号,并从这
个零件,标上记号,并从这![]() 个零件中再抽取
个零件中再抽取![]() 个,求再次抽取的
个,求再次抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com