(本小题主要考查函数的导数、最值、等比数列等基础知识,考查分析问题和解决问题的能力、以及创新意识)
(1)解:∵f(x)=e
x-x,∴f'(x)=e
x-1.令f'(x)=0,得x=0.
∴当x>0时,f'(x)>0,当x<0时,f'(x)<0.
∴函数f(x)=e
x-x在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增.
∴当x=0时,f(x)有最小值1
(2)证明:由(1)知,对任意实数x均有e
x-x≥1,即1+x≤e
x.
令
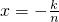
(n∈N
*,k=1,2,,n-1),则
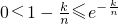
,
∴
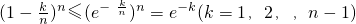
.
即
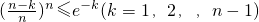
.∵
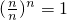
,
∴

.
∵
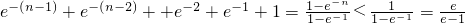
,
∴
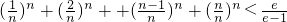
.
分析:(1)若f(x)≥1在x∈R上恒成立,即f(x)的最小值大于等于1,转化为求函数的最小值问题.利用导数求解.
(2)函数导数综合题中,不等式的证明可考虑利用前面得到的函数的性质进行.
点评:本题考查不等式恒成立问题、函数求最值、不等式的证明问题,以及化归转化思想和分类讨论思想,综合性强,难度较大.

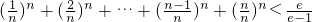
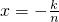 (n∈N*,k=1,2,,n-1),则
(n∈N*,k=1,2,,n-1),则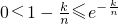 ,
,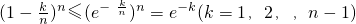 .
.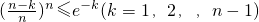 .∵
.∵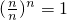 ,
, .
.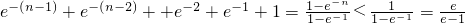 ,
,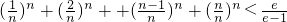 .
.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案