
【题目】随机变量X的分布列为
X | ﹣1 | 0 | 1 | 2 | 3 |
P | 0.16 |
| a2 |
| 0.3 |
(1)求a的值;
(2)求E(X);
(3)若Y=2X﹣3,求E(Y).
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c(b,c∈R),并设 ![]() ,
,
(1)若F(x)图像在x=0处的切线方程为x﹣y=0,求b、c的值;
(2)若函数F(x)是(﹣∞,+∞)上单调递减,则 ①当x≥0时,试判断f(x)与(x+c)2的大小关系,并证明之;
②对满足题设条件的任意b、c,不等式f(c)﹣Mc2≤f(b)﹣Mb2恒成立,求M的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )的四个顶点,四边形
)的四个顶点,四边形![]() 是圆
是圆![]() :
:![]() 的外切平行四边形,其面积为
的外切平行四边形,其面积为![]() .椭圆
.椭圆![]() 的内接
的内接![]() 的重心(三条中线的交点)为坐标原点
的重心(三条中线的交点)为坐标原点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() 的面积是否为定值?若是,求出该定值,若不是,请说明理由.
的面积是否为定值?若是,求出该定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】专家研究表明,![]() 2.5是霾的主要成份,在研究
2.5是霾的主要成份,在研究![]() 2.5形成原因时,某研究人员研究了
2.5形成原因时,某研究人员研究了![]() 2.5与燃烧排放的
2.5与燃烧排放的![]() 、
、![]() 、
、![]() 、
、![]() 等物质的相关关系.下图是某地某月
等物质的相关关系.下图是某地某月![]() 2.5与
2.5与![]() 和
和![]() 相关性的散点图.
相关性的散点图.
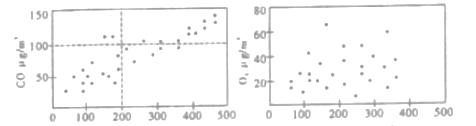
(Ⅰ)根据上面散点图,请你就![]() ,
,![]() 对
对![]() 2.5的影响关系做出初步评价;
2.5的影响关系做出初步评价;
(Ⅱ)根据有关规定,当![]() 排放量低于
排放量低于![]() 时
时![]() 排放量达标,反之为
排放量达标,反之为![]() 排放量超标;当
排放量超标;当![]() 2.5值大于
2.5值大于![]() 时雾霾严重,反之雾霾不严重.根据
时雾霾严重,反之雾霾不严重.根据![]() 2.5与
2.5与![]() 相关性的散点图填写好下面
相关性的散点图填写好下面![]() 列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
雾霾不严重 | 雾霾严重 | 总计 | |
| |||
| |||
总计 |
(Ⅲ)我们知道雾霾对交通影响较大.某市交通部门发现,在一个月内,当![]() 排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,
排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,![]() 排放量是60,120,180的概率一次是
排放量是60,120,180的概率一次是![]() ,
,![]() ,
,![]() (
(![]() ),求该路口一个月的交通流量期望值的取值范围.
),求该路口一个月的交通流量期望值的取值范围.
附:
0.100 | 0.050 | 0.010 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知设函数f(x)=loga(1+2x)﹣loga(1﹣2x)(a>0,a≠1).
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)求使f(x)>0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若偶函数f(x)在(﹣∞,﹣1]上是增函数,则下列关系式中成立的是( )
A.f(﹣ ![]() )<f(﹣1)<f(2)
)<f(﹣1)<f(2)
B.f(﹣1)<f(﹣ ![]() )<f(2)??
)<f(2)??
C.f(2)<f(﹣1)<f(﹣ ![]() )
)
D.f(2)<f(﹣ ![]() )<f(﹣1)
)<f(﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC. 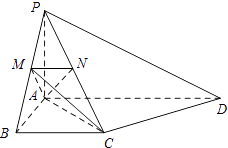
(1)证明:平面AMN⊥平面PBA;
(2)若M为PB的中点,求二面角M﹣AC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com