
分析 (1)曲线C1:ρsin2θ=2acosθ(a>0)化为ρ2sin2θ=2aρcosθ(a>0),把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,代入即可得出;直线C2$\left\{\begin{array}{l}x=-2+\frac{{\sqrt{2}}}{2}t\\ y=4+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),相减即可得出.
(2)把直线C2$\left\{\begin{array}{l}x=-2+\frac{{\sqrt{2}}}{2}t\\ y=4+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数)代入y2=2ax,可得:t2+$(8\sqrt{2}-2\sqrt{2}a)$t+8a+32=0,利用根与系数的关系可得:$({t}_{1}-{t}_{2})^{2}$=$({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}$=8a2-96a.由于|PM|,
|MN|,|PN|成等比数列,可得|MN|2=|PM||PN|,把根与系数代入即可得出.
解答 解:(1)曲线C1:ρsin2θ=2acosθ(a>0)化为ρ2sin2θ=2aρcosθ(a>0),
∴y2=2ax;
直线C2$\left\{\begin{array}{l}x=-2+\frac{{\sqrt{2}}}{2}t\\ y=4+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),相减化为x-y+6=0.
(2)把直线C2$\left\{\begin{array}{l}x=-2+\frac{{\sqrt{2}}}{2}t\\ y=4+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数)代入y2=2ax,可得:t2+$(8\sqrt{2}-2\sqrt{2}a)$t+8a+32=0,
∴t1+t2=$2\sqrt{2}a-8\sqrt{2}$,t1t2=8a+32.
∴$({t}_{1}-{t}_{2})^{2}$=$({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}$=$(2\sqrt{2}a-8\sqrt{2})^{2}-4(8a+32)$=8a2-96a.
∵|PM|,|MN|,|PN|成等比数列,∴|MN|2=|PM||PN|,
∴8a2-96a=8a+32,
化为a2-13a-4=0,a>0,解得a=$\frac{13+\sqrt{185}}{2}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程的应用、一元二次方程的根与系数、等比数列的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{10}$) | B. | (10,+∞) | C. | ($\frac{1}{10}$,10) | D. | (0,$\frac{1}{10}$)∪(10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{3}$) | B. | (-1,-$\frac{1}{3}$] | C. | (-∞,-1)∪[-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x-1≤0 | B. | ?x∈R,2x-1≤0 | C. | ?x∈R,2x-1<0 | D. | ?x∈R,2x-1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
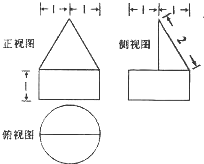
| A. | $\frac{\sqrt{3}π}{6}$+1 | B. | $\frac{\sqrt{3}π}{6}$+π | C. | $\frac{\sqrt{3}π}{3}$+π | D. | $\frac{\sqrt{3}π}{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com