Question

3．设实数x，y满足$\left\{\begin{array}{l}{（2x-y+2）（4x-y-2）≤0}\\{0≤x≤2}\\{y≥0}\end{array}\right.$，若目标函数z=mnx+y（0＜n＜m）的最大值为10，则2m+n的取值范围为（　　）

• A． （4，+∞）
• B． [4，+∞）
• C． [3$\sqrt{2}$，+∞）
• D． （3$\sqrt{2}$，+∞）

Answer 1

分析 作出不等式组对应的平面区域，利用目标函数的最大值确定最优解，联立方程组求得最优解的坐标，代入目标函数求得mn=2，结合已知得到m的范围，然后利用函数单调性即可得到结论．

解答 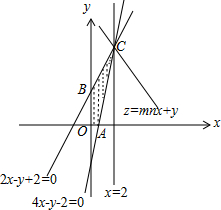解：作出不等式组对应的平面区域如图，
由z=mnx+y（m＞n＞0），
得y=-mnx+z（m＞n＞0），
则由图象可知当直线y=-mnx+z经过点C时，截距最大，此时z最大为10，
由$\left\{\begin{array}{l}{2x-y+2=0}\\{4x-y-2=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$．
即C（2，6），此时2mn+6=10，
即mn=2，
∵m＞n＞0，∴m$＞\sqrt{2}$．
∴2m+n=2m+$\frac{2}{m}$=2（m+$\frac{1}{m}$）$＞2（\sqrt{2}+\frac{\sqrt{2}}{2}）=3\sqrt{2}$．
∴2m+n的取值范围为（$3\sqrt{2}，+∞$）．
故选：D．

点评 本题主要考查线性规划的应用以及利用函数单调性求函数最值，利用数形结合是解决本题的关键，是中档题．