
 已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )
已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )| A. | 8 | B. | 8$\sqrt{3}$ | C. | 16 | D. | 16$\sqrt{3}$ |
分析 先求弦AB长,再求高,即点F2到直线AB的距离.利用平行四边的面积公式进行求解.
解答 解:因为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1,所以a2=16,b2=4,c2=12,F1(-2$\sqrt{3}$,0).
若直线AB的斜率不存在时,即x=-2$\sqrt{3}$,
此时A(-2$\sqrt{3}$,1),B(-2$\sqrt{3}$,-1),故S?ABCD=2×4$\sqrt{3}$=8$\sqrt{3}$;
若直线AB的斜率存在且设为k,即y=k(x+2$\sqrt{3}$),与$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1联立方程组整理得:
(1+4k2)x2+16$\sqrt{3}$k2x+48k2-16=0,有x1+x2=-$\frac{16\sqrt{3}{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{48{k}^{2}-16}{1+4{k}^{2}}$,
则|AB|=$\sqrt{1+{k}^{2}}\left|{x}_{1}-{x}_{2}\right|$=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=8$\sqrt{1+{k}^{2}}\sqrt{\frac{1+{k}^{2}}{(1+4{k}^{2})^{2}}}$.
AB边上高,即点F2(2$\sqrt{3}$,0)到直线y=k(x+2$\sqrt{3}$)的距离为$\frac{\left|4\sqrt{3}k\right|}{\sqrt{1+{k}^{2}}}$,
则S?ABCD=$\left|8\sqrt{3}k\right|\sqrt{\frac{16+16{k}^{2}}{(1+4{k}^{2})^{2}}}$=8$\sqrt{3}\sqrt{\frac{16{k}^{2}+16{k}^{4}}{(1+4{k}^{2})^{2}}}$=8$\sqrt{3}\sqrt{1+\frac{8{k}^{2}-1}{1+8{k}^{2}+16{k}^{4}}}$.
令8k2-1=t,t≥-1,
则8k2=1+t,则$\frac{8{k}^{2}-1}{1+8{k}^{2}+16{k}^{4}}$=$\frac{4t}{{t}^{2}+6t+9}$,
当t=0时,$\frac{4t}{{t}^{2}+6t+9}$=0,S?ABCD=8$\sqrt{3}$.
若t≠0,$\frac{4t}{{t}^{2}+6t+9}$=$\frac{4}{t+\frac{9}{t}+6}$,
则当t=3时,$\frac{4t}{{t}^{2}+6t+9}$取得最大值$\frac{1}{3}$,此时S?ABCD=8$\sqrt{3}$•$\sqrt{\frac{4}{3}}$=16.
综上,(S?ABCD)max=16.
故选:C
点评 本题主要考查平行四边形的面积的计算,考查直线和圆锥曲线的位置关系的应用,联立直线和椭圆的方程是解决本题的关键.综合性较强,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{7}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{5}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,$\overrightarrow{BP}$=$\overrightarrow{DA}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
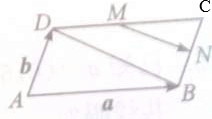 如图,?ABCD中,M、N分别是边DC、BC的中点.
如图,?ABCD中,M、N分别是边DC、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-$\sqrt{3}$) | B. | (-∞,-2)∪($\sqrt{3}$,+∞) | C. | [-3,-$\sqrt{3}$] | D. | (-∞,-2)∪(-$\sqrt{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com