
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 根据条件判断函数的对称性和单调性,结合函数单调性和对称性之间的关系进行转化求解即可.
解答 解:由f(x)=f(2-x),得函数关于x=1对称,
由f'(x)(x-1)>0得,
当x>1时,f′(x)>0,此时函数为增函数,
当x<1时,f′(x)<0,此时函数f(x)为减函数,
若x1<x2,当x2≤1,函数为减函数,满足对任意的x1<x2,f(x1)>f(x2),
此时x1+x2<2,
若x2>1,
∵函数f(x)关于x=1对称,则f(x2)=f(2-x2),
则2-x2<1,
则由f(x1)>f(x2)得f(x1)>f(x2)=f(2-x2),
此时函数在x<1时为减函数,
则x1<2-x2,即x1+x2<2,
即对任意的x1<x2,f(x1)>f(x2)得x1+x2<2,
反之也成立,
即对任意的x1<x2,f(x1)>f(x2)是x1+x2<2的充要条件,
故选:B
点评 本题主要考查充分条件和必要条件的判断,根据条件判断函数的对称性和单调性之间的关系,利用条件进行转化是解决本题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3 ) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
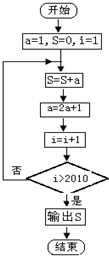 如图是计算首项为1的数列{an}前m项和Sn的算法框图,
如图是计算首项为1的数列{an}前m项和Sn的算法框图,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com