
 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.
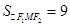 ; (2)
; (2) 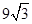 ,
,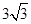 ; (3) θ增大时面积变小,证明过程见解析.
; (3) θ增大时面积变小,证明过程见解析.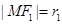 ,
,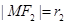 , 直角三角形△F1MF2中
, 直角三角形△F1MF2中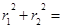
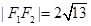 ,利用双曲线定义得
,利用双曲线定义得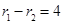 ,平方得
,平方得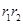 ,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式
,求得面积;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面积公式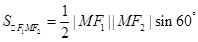 可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系
可得面积;(3) 由双曲线定义与余弦定理,可得面积与θ的关系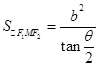 ,所以θ增大时面积变小.
,所以θ增大时面积变小.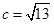 ,
,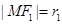 ,
,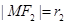 (
(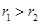 ).
).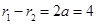 ,两边平方得,
,两边平方得,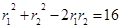 ,
,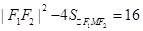 ,
,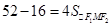 ,求得
,求得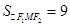 . 4分
. 4分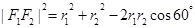 ,
,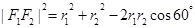 ,所以
,所以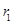
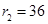 .
.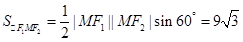 .
.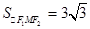 . 8分
. 8分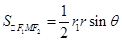 .
.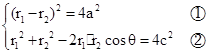
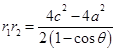 ,
,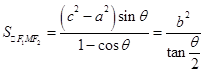 ,
,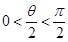 ,
,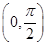 内,
内,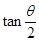 是增函数,
是增函数,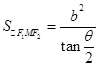 将减小. 12分
将减小. 12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
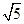 )2+y2=4,(x-
)2+y2=4,(x-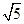 )2+y2=4中的一个内切,另一个外切.
)2+y2=4中的一个内切,另一个外切.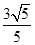 ,
,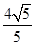 ),F(
),F(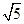 ,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标.
,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
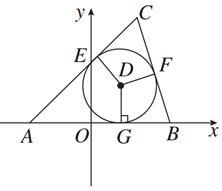
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com