
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望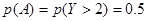 ;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率
;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率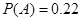 .
. 表示至第2分钟末已买完饭的人数,包括三种情况, 第2分钟末没有人买晚饭,第2分钟末有一人买饭,它包括:第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟,第2分钟末,有两人买饭,故
表示至第2分钟末已买完饭的人数,包括三种情况, 第2分钟末没有人买晚饭,第2分钟末有一人买饭,它包括:第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟,第2分钟末,有两人买饭,故 所有可能的取值为
所有可能的取值为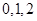 ,分别求出概率,从而写出
,分别求出概率,从而写出 的分布列,求出数学期望.
的分布列,求出数学期望.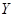 表示学生买饭所需的时间,用频率估计概率,得
表示学生买饭所需的时间,用频率估计概率,得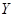 的分布列如下:
的分布列如下: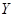 | 1 | 2 | 3 | 4 | 5 |
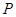 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
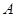 表示事件“第三个学生恰好等待4分钟开始买饭”,则事件A对应三种情形:
表示事件“第三个学生恰好等待4分钟开始买饭”,则事件A对应三种情形: 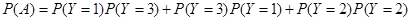
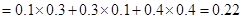 (6分)
(6分) 所有可能的取值为
所有可能的取值为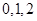
 对应第一个学生买饭所需的时间超过2分钟,
对应第一个学生买饭所需的时间超过2分钟,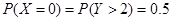
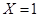 对应第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟.
对应第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟. 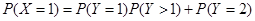
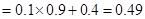
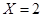 对应两个学生买饭所需时间均为1分钟,
对应两个学生买饭所需时间均为1分钟, 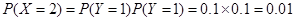
 的分布列为
的分布列为 | 0 | 1 | 2 |
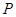 | 0.5 | 0.49 | 0.01 |
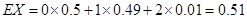 (12分)
(12分)

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题

 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为 (
( ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利 的可能性为
的可能性为 ,亏损
,亏损 的可能性为
的可能性为 ;位于二类风区的B项目获利
;位于二类风区的B项目获利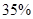 的可能性为
的可能性为 ,亏损
,亏损 的可能性是
的可能性是 ,不赔不赚的可能性是
,不赔不赚的可能性是 .
. 和
和 ,试写出随机变量
,试写出随机变量 与
与 的分布列和期望
的分布列和期望 ,
, ;
; 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时, =0,当四点不共面时,
=0,当四点不共面时, 的值为四点组成的四面体的体积.
的值为四点组成的四面体的体积. =0);
=0); 的分布列,并求其数学期望E (
的分布列,并求其数学期望E ( ).
).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.甲平均击中的环数比乙平均击中的环数多 |
| B.乙平均击中的环数比甲平均击中的环数多 |
| C.甲、乙两人平均击中的环数相等 |
| D.仅依据上述数据,无法判断谁击中的环数多 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.  :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质 的概率;
的概率; ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com