
【题目】在△ABC中,角A,B,C的对边分别为a,b,c, ![]() =
= ![]() .
.
(1)求角C的大小;
(2)求sinAsinB的最大值.
【答案】
(1)解:因为: ![]() =
= ![]() ,
,
所以:由正弦定理可得: ![]() =
= ![]() ,
,
所以:2sinAcosC=﹣(sinBcosC+sinCcosB)=﹣sinA.
因为:sinA≠0,
所以:cosC=﹣ ![]() .
.
又因为:0<C<π,
故C= ![]()
(2)解:因为:sinAsinB=sinAsin( ![]() ﹣A)=sinA(
﹣A)=sinA( ![]() cosA﹣
cosA﹣ ![]() sinA)
sinA)
= ![]() sin2A﹣
sin2A﹣ ![]() sin2A=
sin2A= ![]() sin2A﹣
sin2A﹣ ![]()
= ![]() sin(2A+
sin(2A+ ![]() )﹣
)﹣ ![]() .
.
因为:0<A< ![]() ,
,
所以:当A= ![]() 时,sinAsinB有最大值为
时,sinAsinB有最大值为 ![]()
【解析】(1)由正弦定理,三角形内角和定理,两角和的正弦函数公式,化简已知可得2sinAcosC=﹣sinA,结合sinA≠0,可求cosC=﹣ ![]() ,结合范围0<C<π,可求C的值.(2)由(1)及三角函数恒等变换化简可得sinAsinB=
,结合范围0<C<π,可求C的值.(2)由(1)及三角函数恒等变换化简可得sinAsinB= ![]() sin(2A+
sin(2A+ ![]() )﹣
)﹣ ![]() ,结合范围0<A<
,结合范围0<A< ![]() ,利用正弦函数的图象和性质可求最大值.
,利用正弦函数的图象和性质可求最大值.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】为了调查喜欢看书是否与性别有关,某校调查小组就“是否喜欢看书”这个问题,在全校随机调研了100名学生.
(1)完成下列![]() 列联表:
列联表:
喜欢看书 | 不喜欢看书 | 合计 | |
女生 | 15 | 50 | |
男生 | 25 | ||
合计 | 100 |
(2)能否在犯错率不超过0.025的前提下认为“喜欢看书与性别有关”.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题: 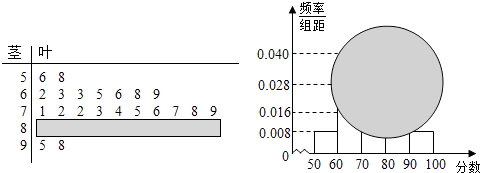
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若规定:75(包含75分)分以上为良好,90分(包含90分)以上为优秀,要从分数在良好以上的试卷中任取两份分析学生失分情况,设在抽取的试卷中,分数为优秀的试卷份数为X,求X的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,M(﹣2,0).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A(ρ,θ)为曲线C上一点,B(ρ,θ+ ![]() ),且|BM|=1.
),且|BM|=1.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)求|OA|2+|MA|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() 与两个定点
与两个定点![]() ,
,![]() 的距离之比为
的距离之比为![]() .
.
(1)求点![]() 的坐标所满足的关系式;
的坐标所满足的关系式;
(2)求![]() 面积的最大值;
面积的最大值;
(3)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com