
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(Ⅰ)在梯形![]() 中,设
中,设![]() ,题意求得
,题意求得![]() ,再由余弦定理求得
,再由余弦定理求得![]() ,满足
,满足![]() ,得则
,得则![]() .再由
.再由![]() 平面
平面![]() 得
得![]() ,由线面垂直的判定可.进一步得到
,由线面垂直的判定可.进一步得到![]() 丄平面
丄平面![]() ;(Ⅱ)分别以直线
;(Ⅱ)分别以直线![]() 为:
为:![]() 轴,
轴,![]() 轴轴建立如图所示的空间直角坐标系,设
轴轴建立如图所示的空间直角坐标系,设![]() ,令
,令![]()
![]() 得到
得到![]() 的坐标,求出平面
的坐标,求出平面![]() 的一法向量.由题意可得平面的
的一法向量.由题意可得平面的![]() 一个法向量,求出两法向量所成角的余弦值,可得当
一个法向量,求出两法向量所成角的余弦值,可得当![]()
![]() 时,有最小值为
时,有最小值为![]() ,此时点
,此时点![]() 与点
与点![]() 重合.
重合.
试题解析:(Ⅰ)证明:在梯形![]() 中,∵
中,∵![]() ,设
,设![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() .则
.则![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,而
,而![]() ,∴
,∴![]() 平面
平面![]() .∵
.∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)解:分别以直线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
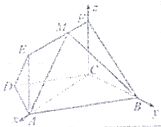
设![]() ,令
,令![]() ,
,
则![]() ,
,
∴![]()
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由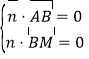 得
得![]() ,取
,取![]() ,则
,则![]() ,
,
∵![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴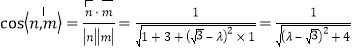
∵![]() ,∴当
,∴当![]() 时,
时,![]() 有最小值为
有最小值为![]() ,
,
∴点![]() 与点
与点![]() 重合时,平面
重合时,平面![]() 与平面
与平面![]() 所成二面角最大,此时二面角的余弦值为
所成二面角最大,此时二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮![]() ,其中P是弧TN上一点.设
,其中P是弧TN上一点.设![]() ,长方形
,长方形![]() 的面积为S平方米.
的面积为S平方米.
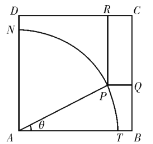
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线与AE、BE分别交于点C、D,其中∠AEB=30°. 
(1)求证: ![]()
(2)求∠PCE的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在城市旧城改造中,某小区为了升级居住环境,拟在小区的闲置地中规划一个面积为![]() 的矩形区域(如图所示),按规划要求:在矩形内的四周安排
的矩形区域(如图所示),按规划要求:在矩形内的四周安排![]() 宽的绿化,绿化造价为200元/
宽的绿化,绿化造价为200元/![]() ,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/
,中间区域地面硬化以方便后期放置各类健身器材,硬化造价为100元/![]() .设矩形的长为
.设矩形的长为![]() .
.
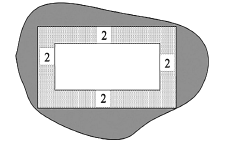
(1)设总造价![]() (元)表示为长度
(元)表示为长度![]() 的函数;
的函数;
(2)当![]() 取何值时,总造价最低,并求出最低总造价.
取何值时,总造价最低,并求出最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了
市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
不支持 | 支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否有![]() 的把握认为支持申办足球世界杯与性别有关;
的把握认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退体老人中随机抽取
位退体老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com