
| A. | (-∞,-2] | B. | (-2,+∞) | C. | (-2,-$\frac{1}{8}$) | D. | $[-\frac{1}{8},+∞)$ |
分析 求出函数的导数,利用导函数的符号,转化求解表达式的最小值,然后推出a的范围.
解答 解:$f'(x)=\frac{1}{x}+2ax=\frac{{2a{x^2}+1}}{x}$,
2ax2+1>0在$({\frac{1}{2},2})$内有解,
所以$a>(-\frac{1}{2{x}^{2}})_{min}$,
由于$x∈({\frac{1}{2},2})$,所以${x^2}∈({\frac{1}{4},4})$,
$(-\frac{1}{{2{x^2}}})∈({-2,-\frac{1}{8}})$,所以a>-2,
故选:B.
点评 本题考查函数的导数的应用,函数恒成立以及函数的最值的求法,考查转化思想以及计算能力.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
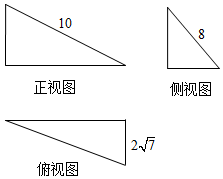
| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{21}{4}$ | C. | $\frac{17}{4}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-{y^2}$=1 | B. | $\frac{y^2}{3}-{x^2}$=1 | C. | y2-$\frac{x^2}{3}$=1 | D. | $\frac{x^2}{2}-\frac{y^2}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
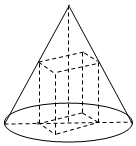 底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com