
分析 根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2,的圆与直线l相切,此时圆心在y轴上,求出A,B的坐标,利用△BPF1∽△BF2P,即可得出结论.
解答 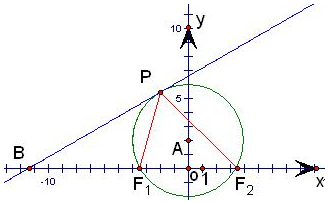 解:根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2,的圆与直线l相切,此时圆心在y轴上,设坐标为A(0,y),则
解:根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2,的圆与直线l相切,此时圆心在y轴上,设坐标为A(0,y),则
$\sqrt{3+{y}^{2}}$=$\frac{|-2y+6|}{\sqrt{7}}$,可得A(0,-2+$\sqrt{21}$)
在直线l:$\sqrt{3}$x-2y+6=0=0中令y=0得B的坐标:
B(-2$\sqrt{3}$,0),
在三角形BPF1和三角形BF2P中,∠BPF1=∠BF2P,
∴△BPF1∽△BF2P,
∴$\frac{{|{P{F_1}}|}}{{|{P{F_2}}|}}$=$\frac{PB}{B{F}_{2}}$=$\frac{9}{3\sqrt{3}}$=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查双曲线的性质,考查直线与圆的位置关系,考查三角形相似的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S△ABC2=S△BCO•S△BCD | B. | S△ABD2=S△BOD•S△BOC | ||
| C. | S△ADC2=S△DOC•S△BOC | D. | S△BDC2=S△ABD•S△ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
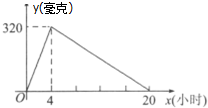 某种新药服用x小时后血液中残留为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
某种新药服用x小时后血液中残留为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )| A. | 上午10:00 | B. | 中午12:00 | C. | 下午4:00 | D. | 下午6:00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com