
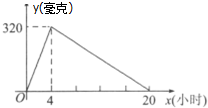
 某种新药服用x小时后血液中残留为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
某种新药服用x小时后血液中残留为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )| A. | 上午10:00 | B. | 中午12:00 | C. | 下午4:00 | D. | 下午6:00 |
分析 由图象分段设出一次函数模型,分别代入点(4,320)和(20,0)求解函数解析式;由第一次服药的残留量大于等于240求解x的范围,同样由第二次服药的残留量大于等于240求解第二次的药效时间.
解答 解:由图象可知:当x∈[0,4]时,设y=kx.
把(4,320)代入,得k=80,∴y=80x.
当x∈[4,320]时,设y=kx+b.
把(4,20),(20,0)代入得$\left\{\begin{array}{l}{4k+b=320}\\{20k+b=20}\end{array}\right.$,解得k=-20,b=400.
∴y=400-20x.
当x∈[0,4]时,80x≥240,解得3≤x≤4;
当x∈[4,320]时,400-20x≥240,解得4<x≤8,
∴3≤x≤8.
故第二次服药应在第一次服药8小时后,即当日16:00,
故选C.
点评 本题考查了函数模型的选择及应用,考查了分段函数涉及的不等式的解法,解答此题的关键是对题意的理解与把握,考查了计算能力,是中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a∈M | B. | a∉M | C. | {a}∈M | D. | {a}∉M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 6π+12 | B. | 6π+24 | C. | 12π+12 | D. | 24π+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com