练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知函数f（x）=x2-2x+a在[2，3]上的最大值与最小值之和为5，则实数a的值为（　　）
    A．1B．2C．3D．4

    分析 根据f（x）开口朝上，对称轴为 x=1，f（x）在[2，3]是单调递增函数，求出函数的最大值与最小值．

    解答 解：由题意知，f（x） 开口朝上，对称轴为 x=1在区间[2，3]左侧，f（x）在[2，3]是单调递增函数；
    ∴f（x）在x=2处取得最小值 f（2）=a，在x=3处取得最大值f（3）=3+a；
    ∴a+3+a=5⇒a=1．
    故选：A．

    点评 本题主要考查了一元二次函数的基本性质与图纸基本特征，属简单题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．经过平面外两点可作与该平面平行的平面个数为0或1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=lnx-ax，（a∈R，x＞0）．
    （1）当a=2时，求函数f（x）的单调区间；
    （2）当a＞0时，求函数f（x）在[1，2]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．x的取值范围为[0，10]，给出如图所示程序框图，输入一个数x．则输出的x（x＜6）的概率为$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

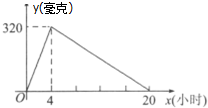    17．某种新药服用x小时后血液中残留为y毫克，如图所示为函数y=f（x）的图象，当血液中药物残留量不小于240毫克时，治疗有效．设某人上午8：00第一次服药，为保证疗效，则第二次服药最迟的时间应为（　　）
    A．上午10：00B．中午12：00C．下午4：00D．下午6：00

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=$\left\{\begin{array}{l}{-x-1（x＜-1）}\\{-{x}^{2}+1（-1≤x≤1）}\\{x-1（x＞1）}\end{array}\right.$．
    （1）求f（2），f（-2）．
    （2）若f（a）=1，求实数a的值．
    （3）判断函数f（x）的奇偶性（只写出结果，不需证明）
    （4）写出函数的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

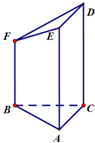    14．几何体ABCDEF如图所示，其中AC⊥AB，AC=3，AB=4，AE、CD、BF均垂直于面ABC，且AE=CD=5，BF=3，则这个几何体的体积为26．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列说法正确的是（　　）
    A．“x＜0”是“ln（x+1）＜0”的充要条件
    B．“?x≥2，x2-3x+2≥0”的否定是“?x＜2，x2-3x+2＜0”
    C．采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5，16，27，38，49的同学均被选出，则该班学生人数可能为60
    D．已知回归直线的斜率的估计值为1.23，样本点的中心为（4，5），则回归直线方程是$\widehat{y}$=1.23x+0.08

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

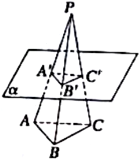    7．已知P为△ABC所在平面外一点，平面α∥平面ABC，且α交线段PA，PB，PC于点A′，B′，C′，若PA′：AA′=2：3，则S△A′B′C′：S△ABC=（　　）
    A．2：3B．2：5C．4：9D．4：25

    查看答案和解析>>

    同步练习册答案