
| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (1,2) |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | S△ABC2=S△BCO•S△BCD | B. | S△ABD2=S△BOD•S△BOC | ||
| C. | S△ADC2=S△DOC•S△BOC | D. | S△BDC2=S△ABD•S△ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
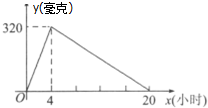 某种新药服用x小时后血液中残留为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
某种新药服用x小时后血液中残留为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )| A. | 上午10:00 | B. | 中午12:00 | C. | 下午4:00 | D. | 下午6:00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
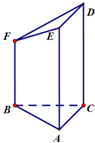 几何体ABCDEF如图所示,其中AC⊥AB,AC=3,AB=4,AE、CD、BF均垂直于面ABC,且AE=CD=5,BF=3,则这个几何体的体积为26.
几何体ABCDEF如图所示,其中AC⊥AB,AC=3,AB=4,AE、CD、BF均垂直于面ABC,且AE=CD=5,BF=3,则这个几何体的体积为26.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
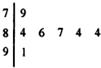 在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )
在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )| A. | 87 | B. | 86 | C. | 85 | D. | 84 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com