
分析 (1)由已知可得a2+c2-b2=$\sqrt{3}$ac,利用余弦定理可求cosB,结合B的范围,即可得解B的值.
(2)利用正弦定理可求sinA,进而可求A.
解答 解:(1)在△ABC中,∵${a^2}+{c^2}-{b^2}-\sqrt{3}ac=0$,
∴a2+c2-b2=$\sqrt{3}$ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\sqrt{3}}{2}$,
∵B∈(0,π),
∴B=$\frac{π}{6}$.
(2)∵$a=\sqrt{3},b=1$,B=$\frac{π}{6}$,
∴由正弦定理可得:sinA=$\frac{asinB}{b}$=$\frac{\sqrt{3}×\frac{1}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
∵a>b,
∴A=$\frac{π}{3}$或$\frac{2π}{3}$.
点评 本题主要考查了正弦定理,余弦定理,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (0,2) | C. | [0,2) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,-2] | B. | [-3,-2) | C. | (-∞,-2] | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
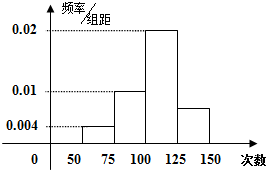 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com