
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC,BD交于点O,PO⊥平面ABCD,PA=AB,E,F,G分别是PO,AD,AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC,BD交于点O,PO⊥平面ABCD,PA=AB,E,F,G分别是PO,AD,AB的中点. 证明:(Ⅰ)∵F,G分别是AD,AB的中点.底面ABCD是正方形,
证明:(Ⅰ)∵F,G分别是AD,AB的中点.底面ABCD是正方形,

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| OP |
| OA |
| OB |
| BP |
| PA |
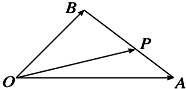
A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
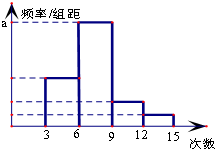 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:| 分组 | 频数 | 频率 |
| [3,6) | 10 | m |
| [6,9) | n | p |
| [9,12) | 4 | q |
| [12,15) | 2 | 0.05 |
| 合计 | N | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
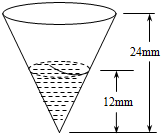 “降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为
“降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com