
下列命题中正确的是 (填上你认为所有正确的选项)
① 空间中三个平面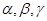 ,若
,若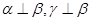 ,则
,则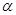 ∥
∥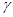
② 空间中两个平面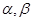 ,若
,若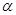 ∥
∥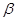 ,直线
,直线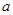 与
与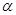 所成角等于直线
所成角等于直线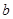 与
与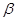 所成角, 则
所成角, 则
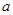 ∥
∥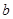 .
.
③ 球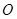 与棱长为
与棱长为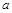 正四面体各面都相切,则该球的表面积为
正四面体各面都相切,则该球的表面积为 ;
;
④ 三棱锥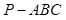 中,
中,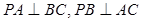 则
则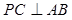 .
.
③④
【解析】
试题分析:结合“墙角结构”,① 空间中三个平面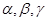 ,若
,若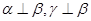 ,则
,则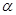 ∥
∥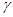 ,不正确;
,不正确;
由直线a,b方向不同时,也能使得,直线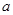 与
与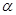 所成角等于直线
所成角等于直线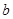 与
与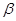 所成角,所以,② 空间中两个平面
所成角,所以,② 空间中两个平面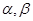 ,若
,若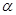 ∥
∥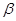 ,直线
,直线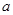 与
与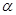 所成角等于直线
所成角等于直线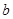 与
与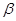 所成角, 则
所成角, 则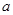 ∥
∥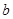 . 不正确;
. 不正确;
棱长为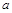 正四面体高为
正四面体高为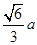 ,设内切球半径为r,正四面体底面积为s,由等积法可得,4×
,设内切球半径为r,正四面体底面积为s,由等积法可得,4×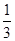 sr=
sr=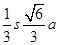 ,
,
r=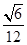 a,该球的表面积为
a,该球的表面积为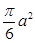 ,③正确。
,③正确。
作PO⊥平面ABC于O,连AO,BO,CO.
因为,PA⊥BC,所以AO⊥BC.
同理,BO⊥CA.
所以,O是△ABC的垂心,CO⊥AB,PC⊥AB. ④正确。故答案为③④。
考点:本题主要考查立体几何中平行关系、垂直关系,四面体的几何性质。
点评:中档题,本题综合性较强,较全面地考查了立体几何的基础知识。对于正四面体,有些结论性的东西,应注意记忆。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com