
分析 (1)先求切线的斜率,再确定切点的坐标,则可写出曲线f(x)在x=1处的切线的点斜式方程;
(2)先确定函数的定义域,再求导,f'(x)=$\frac{2a{x}^{2}-(2a+1)x+1}{x}$,然后由f'(x)>0,得到单调增区间,由f'(x)<0,得到单调减区间.在解不等式时,需对参数a进行分类讨论.
(3)根据条件,可知x1,x2是方程2x2-bx+1=0得两个根,故${x}_{1}{x}_{2}=\frac{1}{2}$.记g(x)=2x2-bx+1,由于b>3时,$g(\frac{1}{2})=\frac{3-b}{2}<0$,g(1)=3-b<0,故${x}_{1}∈(0,\frac{1}{2})$,x2∈(1,+∞).再利用${{b{x}_{i}=2x}_{i}}^{2}+1,{x}_{1}=\frac{1}{2{x}_{2}}$进行化简消元,得f(x1)-f(x2)=${{x}_{2}}^{2}-\frac{1}{4{{x}_{2}}^{2}}-ln(2{{x}_{2}}^{2}),{x}_{2}∈(1,+∞)$.令t=$2{{x}_{2}}^{2}$,构造新的函数h(t)=$\frac{t}{2}-\frac{1}{2t}-lnt$
,然后利用导数判断函数h(t)在(2,+∞)上单调递增,故h(t)>h(2)=$\frac{3}{4}-ln2$,即$f({x}_{1})-f({x}_{2})>\frac{3}{4}-ln2$.
解答 解:(1)a=b=1时,f(x)=x2-x+lnx,f'(x)=2x-1+$\frac{1}{x}$,
x=1时,f(1)=0,f'(1)=2,
故f(x)在x=1处的切线为y=2(x-1),即y=2x-2.
(2)b=2a+1时,f(x)=ax2-(2a+1)x+lnx,定义域为(0,+∞),
f'(x)=$2ax-(2a+1)+\frac{1}{x}$=$\frac{2a{x}^{2}-(2a+1)x+1}{x}$
Ⅰ)、a=0时,f'(x)=$\frac{1-x}{x}$,
由f'(x)>0,得0<x<1;由f'(x)<0,得x>1,
故y=f(x)的单调增区间为(0,1),单调减区间为(1,+∞).
Ⅱ)、a≠0时,f'(x)=$\frac{2a(x-\frac{1}{2a})(x-1)}{x}$,
①a<0时,由f'(x)<0,得x>1;由f'(x)>0,得0<x<1,
故y=f(x)的单调增区间为(0,1),单调减区间为(1,+∞);
②0<a<$\frac{1}{2}$时,$\frac{1}{2a}>1$,
由f'(x)>0,得0<x<1,或x>$\frac{1}{2a}$;由f'(x)<0,得1<x<$\frac{1}{2a}$,
故y=f(x)的单调增区间为(0,1),($\frac{1}{2a}$,+∞),单调减区间为(1,$\frac{1}{2a}$);
③a=$\frac{1}{2}$时,f'(x)=$\frac{(x-1)^{2}}{x}$≥0恒成立,
故y=f(x)的单调增区间为(0,+∞),无单调递减区间;
④$a>\frac{1}{2}$时,$\frac{1}{2a}<1$,
由f'(x)>0,得0<x<$\frac{1}{2a}$,或x>1;由f'(x)<0,得$\frac{1}{2a}<x<1$,
故y=f(x)的单调增区间为(0,$\frac{1}{2a}$),(1,+∞),单调减区间为($\frac{1}{2a}$,1).
(3)a=1时,f(x)=x2-bx+lnx,f'(x)=2x-b+$\frac{1}{x}$=$\frac{2{x}^{2}-bx+1}{x}$,
由题意知,x1,x2是方程2x2-bx+1=0得两个根,故${x}_{1}{x}_{2}=\frac{1}{2}$,
记g(x)=2x2-bx+1,因为b>3,所以$g(\frac{1}{2})=\frac{3-b}{2}<0$,g(1)=3-b<0,
所以${x}_{1}∈(0,\frac{1}{2}),{x}_{2}∈(1,+∞)$,且$b{x}_{1}=2{{x}_{1}}^{2}+1,b{x}_{2}=2{{x}_{2}}^{2}+1$,
f(x1)-f(x2)=$({{x}_{1}}^{2}-{{x}_{2}}^{2})$-(bx1-bx2)+ln$\frac{{x}_{1}}{{x}_{2}}$=-$({{x}_{1}}^{2}-{{x}_{2}}^{2})+ln\frac{{x}_{1}}{{x}_{2}}$,
因为${x}_{1}{x}_{2}=\frac{1}{2}$,所以${x}_{1}=\frac{1}{{2x}_{2}}$,
故f(x1)-f(x2)=${{x}_{2}}^{2}-\frac{1}{4{{x}_{2}}^{2}}-ln(2{{x}_{2}}^{2}),{x}_{2}∈(1,+∞)$,
令t=$2{{x}_{2}}^{2}$∈(2,+∞),h(t)=f(x1)-f(x2)=$\frac{t}{2}-\frac{1}{2t}-lnt$,
因为h'(t)=$\frac{(t-1)^{2}}{2{t}^{2}}≥0$,所以h(t)在(2,+∞)上单调递增,
所以h(t)>h(2)=$\frac{3}{4}-ln2$,即$f({x}_{1})-f({x}_{2})>\frac{3}{4}-ln2$.
点评 本题考查了利用导数求曲线上某点处的切线,利用导数研究函数的单调性,以及不等式的证明.解题过程中运用了等价转化方法、分类讨论的思想方法,还考查了学生构造函数解决问题的能力和计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<k<$\frac{9}{8}$ | B. | 0≤k<$\frac{9}{8}$ | C. | 0<k≤$\frac{9}{8}$ | D. | k≥$\frac{9}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {1,3,5} | C. | {2,4,5} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
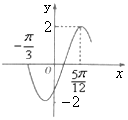 已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则把函数f(x)的图象向左平移$\frac{π}{6}$后得到的函数图象的解析式是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则把函数f(x)的图象向左平移$\frac{π}{6}$后得到的函数图象的解析式是( )| A. | y=2sin2x | B. | y=2sin(2x-$\frac{π}{3}$) | C. | y=2sin(2x-$\frac{π}{6}$) | D. | y=2sin(x-$\frac{π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com