
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用函数的奇偶性和单调性,可判断(1);利用诱导公式,可判断(2);利用正弦定理,可判断(3);判断出三角形的形状,可判断(4).
解答 解:∵f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
故f(x)在[0,1]上是减函数,
故当a,b∈[-1,1]时,有|a|<|b|,则f(|a|)>f(|b|);
当|θ|∈($\frac{π}{4},\frac{π}{2}$)时,1>|sinθ|>|cosθ|>0;
∴f(sinθ)<f(cosθ),故(1)错误;
若锐角α、β满足cosα=sin($\frac{π}{2}$-α)<sinβ,
则$\frac{π}{2}$-α<β,即α+β>$\frac{π}{2}$,故(2)错误;
在△ABC中,如果A>B?a>b?2RsinA>2RsinB?sinA>sinB成立,故(3)正确;
在△ABC中,如果有sin2A=sin2B,
则2A=2B,或2A+2B=π,
即A=B,或C=$\frac{π}{2}$
则该三角形一定为等腰三角形或直角三角形,故(4)错误;
故选:A.
点评 本题以命题的真假判断与应用为载体,考查了函数的图铃和性质,诱导公式,三角函数的单调性,正弦定理,难度中档.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 18种 | C. | 24种 | D. | 30种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
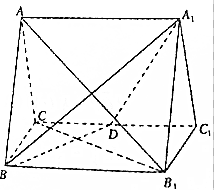 如图,正三棱柱ABC-A1B1C1的所有棱长都有2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都有2,D为CC1中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com