
分析 (1)由题意:定义域R上满足f(-x)=-f(x),可知函数f(x)是奇函数,根据当x∈[0,2]时,f(x)=-x2+2x;当x∈(2,+∞)时,f(x)=2x-4.即可求f(x)的在定义域R上解析式
(2)根据(1)的解析式定义域范围,当x≥0时,讨论,再解关于x的不等式f(x+1)>f(x)即可.
解答 解:(1)由题意:定义域R上满足f(-x)=-f(x),可知函数f(x)是奇函数,
当x∈[0,2]时,即0≤x≤2时,f(x)=-x2+2x;
那么:-2≤x≤0时,则0≤-x≤2,f(-x)=-x2-2x=-f(x),
∴f(x)=x2+2x;
当x∈(2,+∞)时,即:x>2时,f(x)=2x-4.
那么:x<-2时,则-x>2,f(-x)=-2x-4=-f(x),
∴f(x)=2x+4;
故得f(x)的在定义域R上解析式为:f(x)=$\left\{\begin{array}{l}{2x-4,(x>2)}\\{-{x}^{2}+2x,(0≤x≤2)}\\{{x}^{2}+2x,(-2≤x<0)}\\{2x+4,(x<-2)}\end{array}\right.$
(2)∵x≥0,
∴f(x)=$\left\{\begin{array}{l}{2x-4,(x>2)}\\{-{x}^{2}+2x,(0≤x≤2)}\end{array}\right.$
当x>2时,不等式f(x+1)>f(x)等价于:x+1>x,
解得:x>2,
当0≤x≤x+1≤2时,不等式f(x+1)>f(x)等价于:-(x+1)2+2(x+1)>-x2+2x,
解得:$0≤x<\frac{1}{2}$,
当0≤x≤2≤x+1时,不等式f(x+1)>f(x)等价于:2(x+1)-4>-x2+2x,
解得:$\sqrt{2}<x≤2$,
综上所得:当x≥0时,不等式f(x+1)>f(x)的解集为:[0,$\frac{1}{2}$)∪($\sqrt{2}$,+∞).
点评 本题考查了分段函数的解析式的求法,分段函数在不等式中的讨论的运用.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {1,3,5} | C. | {2,4,5} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α>β,则sinα>sinβ | |
| B. | 数列{an},{bn}为等比数列,则数列{an+bn}为等比数列 | |
| C. | 函数f(x),g(x)均为增函数,则函数f(x)•g(x)为增函数 | |
| D. | 在△ABC中,若a>b,则sinA>sinB |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
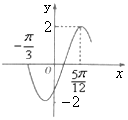 已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则把函数f(x)的图象向左平移$\frac{π}{6}$后得到的函数图象的解析式是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则把函数f(x)的图象向左平移$\frac{π}{6}$后得到的函数图象的解析式是( )| A. | y=2sin2x | B. | y=2sin(2x-$\frac{π}{3}$) | C. | y=2sin(2x-$\frac{π}{6}$) | D. | y=2sin(x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | A?B | C. | B?A | D. | A∩B=∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com