
| 1 |
| 3 |
| 2 |
| 3 |
2
| ||
| 5 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
2
| ||
| 5 |
2
| ||
| 5 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
| OM |
| 1 |
| 3 |
| AO |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| x2 |
| 9 |
| y2 |
| 16 |
| PF1 |
| PF2 |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 9-k |
| y2 |
| 25-k |
查看答案和解析>>
科目:高中数学 来源:2011年福建师大附中高二第一学期期末数学理卷 题型:填空题
以下四个命题中:
 ①“若对所有满足
①“若对所有满足 的
的 ,都有
,都有 ”的否命题;
”的否命题;
② 若直线
若直线 的方向向量为
的方向向量为 =(1,
=(1, ,2),平面
,2),平面 的法向量为
的法向量为 =(-2,0,1),
=(-2,0,1),
则 ∥
∥ .
.
③ 曲线
曲线 与曲线
与曲线 (0﹤k﹤9)有相同的焦点;
(0﹤k﹤9)有相同的焦点;
④ 是空间四点,若
是空间四点,若 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么 四点共面;其中真命题的序号为*****.
四点共面;其中真命题的序号为*****.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| OM |
| 1 |
| 3 |
| AO |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| x2 |
| 9 |
| y2 |
| 16 |
| PF1 |
| PF2 |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 9-k |
| y2 |
| 25-k |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年福建师大附中高二(上)期末数学试卷(理科)(解析版) 题型:填空题
 =
=
 +
+
 +
+
 ,则点M与点A、B、C共面;
,则点M与点A、B、C共面; -
-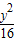 =1的两焦点为F1、F2,点P为双曲线上一点,且
=1的两焦点为F1、F2,点P为双曲线上一点,且 •
• =0,则△PF1F2的面积为16;
=0,则△PF1F2的面积为16; +
+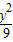 =1与曲线
=1与曲线 +
+ =1(0<k<9)有相同的焦点;
=1(0<k<9)有相同的焦点;查看答案和解析>>
科目:高中数学 来源:2011年福建师大附中高二第一学期期末数学理卷 题型:填空题
以下四个命题中: ①“若对所有满足
①“若对所有满足 的
的 ,都有
,都有 ”的否命题;
”的否命题;
② 若直线
若直线 的方向向量为
的方向向量为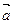 =(1,
=(1, ,2),平面
,2),平面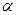 的法向量为
的法向量为 =(-2,0,1),
=(-2,0,1),
则 ∥
∥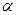 .
.
③ 曲线
曲线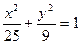 与曲线
与曲线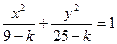 (0﹤k﹤9)有相同的焦点;
(0﹤k﹤9)有相同的焦点;
④ 是空间四点,若
是空间四点,若 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么 四点共面;其中真命题的序号为*****.
四点共面;其中真命题的序号为*****.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com