
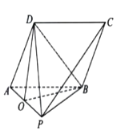
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,由已知可证
,由已知可证![]() ,
,![]() ,可得
,可得![]() 平面
平面![]() ,可证
,可证![]() 。
。
由已知可得![]() 是等腰三角形,分别以
是等腰三角形,分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,求出面
,求出面![]() 与面
与面![]() 的一个法向量,由两法向量所成角的余弦值得二面角
的一个法向量,由两法向量所成角的余弦值得二面角![]() 的余弦值。
的余弦值。
解:(1)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() .
.
由![]() ,
,![]() 知,
知,![]() ,
,![]() .
.
又![]() ∴
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)法一:由题可得![]() ,
,![]() ,故
,故![]() ,所以
,所以![]() .
.
所以可以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
 即
即 令
令![]() 得
得![]() .
.
同理可得平面![]() 的一个法向量为
的一个法向量为![]() .
.
∴![]() .
.
又二面角![]() 为锐二面角所以二面角
为锐二面角所以二面角![]() 的余弦为
的余弦为![]() .
.
法二:设二面角![]() ,
,![]() 的大小分别为
的大小分别为![]() ,
,![]() ,则
,则
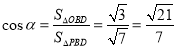 ,
,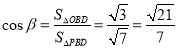 ,
,
∴![]() .
.
即二面角![]() 的余弦为
的余弦为![]() .
.
而二面角![]() 与二面角
与二面角![]() 大小互补、故二面角
大小互补、故二面角![]() 的余弦为
的余弦为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,射线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以O为极点,x轴的正半轴为极轴建立极坐标系,曲线
为参数).以O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与
与![]() 的交点为P(点P不为极点),
的交点为P(点P不为极点),![]() 与
与![]() 的交点为Q,当
的交点为Q,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年入夏以来,我市天气反复,降雨频繁.在下图中统计了上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是()
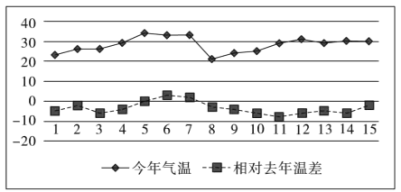
A.今年每天气温都比去年气温高B.今年的气温的平均值比去年低
C.去年8-11号气温持续上升D.今年8号气温最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆G:x2+y2-x-![]() y=0,经过椭圆
y=0,经过椭圆![]() 的右焦点F及上顶点B,过圆外一点(m,0)(m>a)且倾斜角为
的右焦点F及上顶点B,过圆外一点(m,0)(m>a)且倾斜角为![]() 的直线l交椭圆于C,D两点.
的直线l交椭圆于C,D两点.
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的参数方程为:
的参数方程为: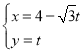 (
(![]() 为参数).
为参数).
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,已知点
,已知点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com