
【题目】已知函数f(x)=x3﹣3x
(1)讨论f(x)的单调区间;
(2)若函数g(x)=f(x)﹣m在[﹣ ![]() ,3]上有三个零点,求实数m的取值范围;
,3]上有三个零点,求实数m的取值范围;
(3)设函数h(x)=ex﹣ex+4n2﹣2n(e为自然对数的底数),如果对任意的x1 , x2∈[ ![]() ,2],都有f(x1)≤h(x2)恒成立,求实数n的取值范围.
,2],都有f(x1)≤h(x2)恒成立,求实数n的取值范围.
【答案】
(1)解:f(x)的定义域为R,f′(x)=3x2﹣3=3(x+1)(x﹣1).
因为当x<﹣1或x>1时,f′(x)>0;当﹣1<x<1时,f′(x)<0;
所以f(x)的单调递增区间为(﹣∞,﹣1)和(1,+∞),单调递减区间为(﹣1,1)
(2)解:要使函数g(x)=f(x)﹣m在[- ![]() ,3]上有三个零点,就是要方程f(x)﹣m=0在[-
,3]上有三个零点,就是要方程f(x)﹣m=0在[- ![]() ,3]上有三个实根,也就是只要函数y=f(x)和函数y=m的图像在[﹣
,3]上有三个实根,也就是只要函数y=f(x)和函数y=m的图像在[﹣ ![]() ,3]上有三个不同的交点.
,3]上有三个不同的交点.
由(1)知,f(x)在(﹣∞,﹣1)和(1,+∞)上单调递增,在(﹣1,1)上单调递减;
所以f(x)在x=﹣1处取得极大值f(﹣1)=2,在x=1处取得极小值f(1)=﹣2.
又f(- ![]() )=
)= ![]() ,f(3)=18.
,f(3)=18.
故实数m的取值范围为 ![]()
(3)解:对任意的 ![]() ,都有f(x1)≤h(x2)恒成立,等价于当
,都有f(x1)≤h(x2)恒成立,等价于当 ![]() 时,f(x)max≤h(x)min成立.
时,f(x)max≤h(x)min成立.
由(1)知,f(x)在[ ![]() ,1]上单调递减,在[1,2]上单调递增,且
,1]上单调递减,在[1,2]上单调递增,且 ![]() ,f(2)=2,所以f(x)在[
,f(2)=2,所以f(x)在[ ![]() ,2]上的最大值f(x)max=2.
,2]上的最大值f(x)max=2.
又h′(x)=ex﹣e,令h′(x)=0,得x=1.
因为当x<1时,h′(x)<0;当x>1时,h′(x)>0;所以h(x)在[ ![]() ,1]上单调递减,在[1,2]上单调递增;故h(x)在[
,1]上单调递减,在[1,2]上单调递增;故h(x)在[ ![]() ,2]上的最小值h(x)min=h(1)=4n2﹣2n.
,2]上的最小值h(x)min=h(1)=4n2﹣2n.
所以4n2﹣2n≥2,解得 ![]() 或n≥1,故实数n的取值范围是(﹣∞,﹣
或n≥1,故实数n的取值范围是(﹣∞,﹣ ![]() ]∪[1,+∞)
]∪[1,+∞)
【解析】(1)直接求导数,然后解不等式可得原函数的增减区间;(2)利用数形结合,将问题转化为函数y=f(x)与y=m的交点问题,只需利用导数研究函数y=f(x)的极值、最值即可;(3)因为h(x)与f(x)是两个不同的函数,所以该不等式恒成立只需f(x)max≤h(x)min即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ![]() ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ![]() ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 并且满足2Sn=an2+n,an>0(n∈N*).
(1)求a1 , a2 , a3;
(2)猜想{an}的通项公式,并加以证明;
(3)设x>0,y>0,且x+y=1,证明: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() ,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
(1)若椭圆C过点 ,且右准线方程为
,且右准线方程为![]() ,求椭圆C的方程;
,求椭圆C的方程;
(2)若直线BN的斜率是直线AM斜率的2倍,求椭圆C的离心率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图由图中数据可知身高在[120,130]内的学生人数为( )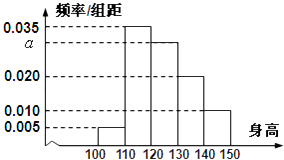
A.20
B.25
C.30
D.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35
B.0.25
C.0.20
D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1 , B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1 , B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1 . 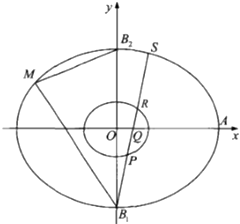
(1)(i)求C的方程;
(ii)求证:C1与C相似;
(2)过B1点任作一直线,自下至上依次与C1、x轴的正半轴、C交于不同的四个点P,Q,R,S,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com