
【题目】设数列{an}的前n项和为Sn , 并且满足2Sn=an2+n,an>0(n∈N*).
(1)求a1 , a2 , a3;
(2)猜想{an}的通项公式,并加以证明;
(3)设x>0,y>0,且x+y=1,证明: ![]() ≤
≤ ![]() .
.
【答案】
(1)解:分别令n=1,2,3,得 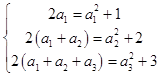
∵an>0,∴a1=1,a2=2,a3=3.
(2)证法一:猜想:an=n,
由2Sn=an2+n①
可知,当n≥2时,2Sn﹣1=an﹣12+(n﹣1)②
①﹣②,得2an=an2﹣an﹣12+1,即an2=2an+an﹣12﹣1.
1)当n=2时,a22=2a2+12﹣1,∵a2>0,∴a2=2;
2)假设当n=k(k≥2)时,ak=k.那么当n=k+1时,
ak+12=2ak+1+ak2﹣1=2ak+1+k2﹣1[ak+1﹣(k+1)][ak+1+(k﹣1)]=0,
∵ak+1>0,k≥2,
∴ak+1+(k﹣1)>0,
∴ak+1=k+1.这就是说,当n=k+1时也成立,
∴an=n(n≥2).显然n=1时,也适合.
故对于n∈N*,均有an=n.
证法二:猜想:an=n,
1)当n=1时,a1=1成立;
2)假设当n=k时,ak=k.
那么当n=k+1时,2Sk+1=ak+12+k+1.∴2(ak+1+Sk)=ak+12+k+1,
∴ak+12=2ak+1+2Sk﹣(k+1)=2ak+1+(k2+k)﹣(k+1)=2ak+1+(k2﹣1)
(以下同证法一)
(3)证法一:要证 ![]() ≤
≤ ![]() ,
,
只要证 ![]() ≤2(n+2),
≤2(n+2),
即n(x+y)+2+ ![]() ≤2(n+2),
≤2(n+2),
将x+y=1代入,得 ![]() ≤n+2,
≤n+2,
即要证4(n2xy+n+1)≤(n+2)2,即4xy≤1.
∵x>0,y>0,且x+y=1,∴ ![]() ≤
≤ ![]() ,
,
即xy≤ ![]() ,故4xy≤1成立,所以原不等式成立.
,故4xy≤1成立,所以原不等式成立.
证法二:∵x>0,y>0,且x+y=1,∴ ![]() ≤
≤ ![]() ①
①
当且仅当 ![]() 时取“=”号.
时取“=”号.
∴ ![]() ≤
≤ ![]() ②
②
当且仅当 ![]() 时取“=”号.
时取“=”号.
① +②,得( ![]() )
) ![]() ≤
≤ ![]() =n+2,
=n+2,
当且仅当 ![]() 时取“=”号.
时取“=”号.
∴ ![]() ≤
≤ ![]() .
.
证法三:可先证 ![]() ≤
≤ ![]() .
.
∵ ![]() ,
, ![]() ,a+b≥
,a+b≥ ![]() ,
,
∴2a+2b≥ ![]() ,
,
∴ ![]() ≥
≥ ![]() ,当且仅当a=b时取等号.
,当且仅当a=b时取等号.
令a=nx+1,b=ny+1,即得: ![]() ≤
≤ ![]() =
= ![]() ,
,
当且仅当nx+1=ny+1即 ![]() 时取等号
时取等号
【解析】(1)分别令n=1,2,3,列出方程组,能够求出求a1 , a2 , a3;(2)证法一:猜想:an=n,由2Sn=an2+n可知,当n≥2时,2Sn﹣1=an﹣12+(n﹣1),所以an2=2an+an﹣12﹣1再用数学归纳法进行证明;证法二:猜想:an=n,直接用数学归纳法进行证明.(3)证法一:要证 ![]() ≤
≤ ![]() ,只要证n(x+y)+2+
,只要证n(x+y)+2+ ![]() ≤2(n+2),将x+y=1代入,得
≤2(n+2),将x+y=1代入,得 ![]() ≤n+2,即要证4xy≤1.由均值不等式知4xy≤1成立,所以原不等式成立.
≤n+2,即要证4xy≤1.由均值不等式知4xy≤1成立,所以原不等式成立.
证法二:由题设知 ![]() ≤
≤ ![]() ,
, ![]() ≤
≤ ![]() ,所以(
,所以( ![]() )
) ![]() ≤
≤ ![]() =n+2,由此可导出
=n+2,由此可导出 ![]() ≤
≤ ![]() .
.
证法三:先证 ![]() ≤
≤ ![]() ,然后令a=nx+1,b=ny+1,即得:
,然后令a=nx+1,b=ny+1,即得: ![]() ≤
≤ ![]() =
= ![]() .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sin
=(sin ![]() x,cos
x,cos ![]() x),
x), ![]() =(sin
=(sin ![]() x,
x, ![]() sin
sin ![]() x),x∈R,函数f(x)=
x),x∈R,函数f(x)= ![]() ,求:
,求:
(1)f(x)的最小正周期;
(2)f(x)在区间[0,1]上的最大值和最小值,以及取得最大值和最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关.”出现这种现象是大家受法不责众的“从众”心理影响,从而不顾及交通安全.某校对全校学生过马路方式进行调查,在所有参与调查的人中,“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n人,已知“跟从别人闯红灯”的人中抽取45人,求n的值;
(2)在“带头闯红灯”的人中,将男生的200人编号为1,2,…,200;将女生的300人编号为201,202,…,500,用系统抽样的方法抽取4人参加“文明交通”宣传活动,若抽取的第一个人的编号为100,把抽取的4人看成一个总体,从这4人中任选取2人,求这两人均是女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx﹣cosx+x+1,x∈[0,2π]
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)的极小值和最大值,并写明取到极小值和最大值时分别对应x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x
(1)讨论f(x)的单调区间;
(2)若函数g(x)=f(x)﹣m在[﹣ ![]() ,3]上有三个零点,求实数m的取值范围;
,3]上有三个零点,求实数m的取值范围;
(3)设函数h(x)=ex﹣ex+4n2﹣2n(e为自然对数的底数),如果对任意的x1 , x2∈[ ![]() ,2],都有f(x1)≤h(x2)恒成立,求实数n的取值范围.
,2],都有f(x1)≤h(x2)恒成立,求实数n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com