
【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关.”出现这种现象是大家受法不责众的“从众”心理影响,从而不顾及交通安全.某校对全校学生过马路方式进行调查,在所有参与调查的人中,“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n人,已知“跟从别人闯红灯”的人中抽取45人,求n的值;
(2)在“带头闯红灯”的人中,将男生的200人编号为1,2,…,200;将女生的300人编号为201,202,…,500,用系统抽样的方法抽取4人参加“文明交通”宣传活动,若抽取的第一个人的编号为100,把抽取的4人看成一个总体,从这4人中任选取2人,求这两人均是女生的概率.
【答案】
(1)解:由题意得, ![]() ,
,
解得n=100
(2)解:由系统抽样得到的号码分别为100,225,350,475.
其中100号为男生,设为A,而225,350,475都为女生,分别设为B1,B2,B3,
从这4人中任选取2人所有的基本事件为:(AB1),(AB2),(AB3),(B1B2),(B1B3),(B2B3),共有6个.这两人均是女生的基本事件为(B1B2),(B1B3),(B2B3),共有3个.故从这4人中任选取2人,这两人均是女生的概率为 ![]() .
.
【解析】(1)由题意利用分层抽样的性质列出方程,由此能求出n的值.(2)由系统抽样得到的号码分别为100,225,350,475,其中100号为男生,设为A,而225,350,475都为女生,分别设为B1 , B2 , B3 , 由此利用列举法能求出从这4人中任选取2人,这两人均是女生的概率.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ),且
),且![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若函数![]() 在区间
在区间![]() 内有且仅有一个极值点,求
内有且仅有一个极值点,求![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() (
(![]() )为两曲线
)为两曲线![]() (
(![]() ),
),![]() 的交点,且两曲线在交点
的交点,且两曲线在交点![]() 处的切线分别为
处的切线分别为![]() ,
, ![]() .若取
.若取![]() ,试判断当直线
,试判断当直线![]() ,
, ![]() 与
与![]() 轴围成等腰三角形时
轴围成等腰三角形时![]() 值的个数并说明理由.
值的个数并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ![]() ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ![]() ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
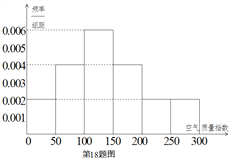
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 并且满足2Sn=an2+n,an>0(n∈N*).
(1)求a1 , a2 , a3;
(2)猜想{an}的通项公式,并加以证明;
(3)设x>0,y>0,且x+y=1,证明: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com