
 ,
, .
. ,若
,若 ,求
,求 的值;
的值; ,当
,当 时,求
时,求 在
在 上的最小值;
上的最小值; 在区间
在区间 上的最大值.
上的最大值.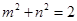 ;(Ⅱ)当
;(Ⅱ)当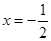 时,
时, 最小值为
最小值为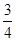 ;(Ⅲ)当
;(Ⅲ)当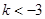 时,
时,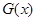 在
在 上的最大值为0;当
上的最大值为0;当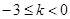 时,
时,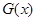 在
在 上的最大值为
上的最大值为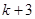 ;当
;当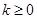 时,
时,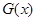 在
在 上的最大值为
上的最大值为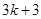 .
.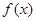 去掉绝对值写成分段函数形式,结合函数图像满足
去掉绝对值写成分段函数形式,结合函数图像满足 的
的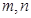 只可能为
只可能为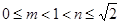 ,从而
,从而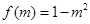 ,
,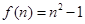 ,由
,由 即可得
即可得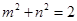 ;(Ⅱ)写出
;(Ⅱ)写出 的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为
的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为  的最小值;(Ⅲ)将
的最小值;(Ⅲ)将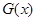 写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.
写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.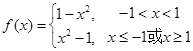
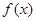 图像可知,
图像可知,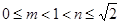
 即为
即为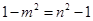 ,所以
,所以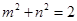 3分
3分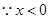 ,则
,则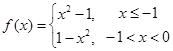 ,
,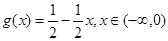
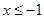 时,
时,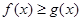 ,即为
,即为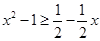 ,解得
,解得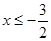
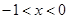 时,
时,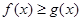 ,即为
,即为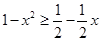 ,解得
,解得
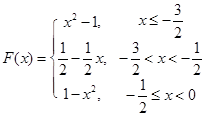
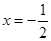 时,
时, 最小值为
最小值为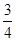
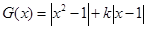
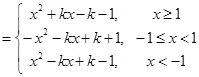
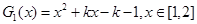 ,结合图像可知,
,结合图像可知,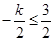 ,即
,即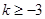 时,
时,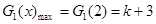
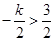 ,即
,即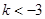 时,
时,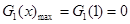 8分
8分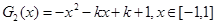 ,结合图像可知,
,结合图像可知,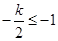 ,即
,即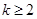 时,
时,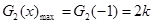
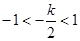 ,即
,即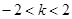 时,
时,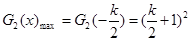
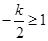 ,即
,即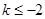 时,
时,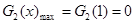
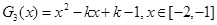 ,结合图像可知,
,结合图像可知,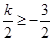 ,即
,即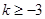 时,
时,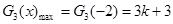
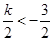 ,即
,即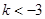 时,
时,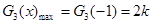 10分
10分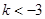 时,
时,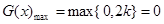
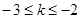 时,
时,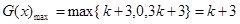
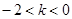 时,
时,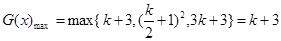
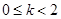 时,
时,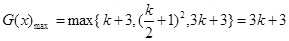
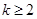 时,
时,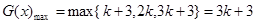 15分
15分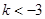 时,
时,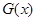 在
在 上的最大值为0
上的最大值为0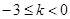 时,
时,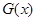 在
在 上的最大值为
上的最大值为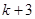
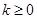 时,
时,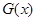 在
在 上的最大值为
上的最大值为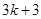 . 16分
. 16分

 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:不详 题型:解答题
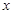 元,
元,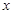 为整数.
为整数.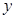 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格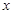 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);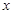 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润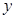 (元)最大,并求出最大值.
(元)最大,并求出最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com