
分析 由a1,a2,a3均为正数,且a1+a2+a3=1,运用乘1法和三元均值不等式,以及不等式的性质,即可得证.
解答 证明:因为a1,a2,a3均为正数,且a1+a2+a3=1,
所以$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}$=$({a_1}+{a_2}+{a_3})({\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}})$
$≥3{({{a_1}{a_2}{a_3}})^{\frac{1}{3}}}•3{({\frac{1}{a_1}\frac{1}{a_2}\frac{1}{a_3}})^{\frac{1}{3}}}=9$,
(当且仅当${a_1}={a_2}={a_3}=\frac{1}{3}$时等号成立)
所以$\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}≥9$.
点评 本题考查不等式的证明,注意运用三元均值不等式和不等式的性质,考查推理能力,属于基础题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy,设点M(x0,y0)是椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1上一点,从原点O向圆M:(x-x0)2+(y-y0)2=r2作两条切线分别与椭圆C交于点P、Q,直线OP,OQ的斜率分别记为k1,k2.
如图,在平面直角坐标系xOy,设点M(x0,y0)是椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1上一点,从原点O向圆M:(x-x0)2+(y-y0)2=r2作两条切线分别与椭圆C交于点P、Q,直线OP,OQ的斜率分别记为k1,k2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1(x<-2) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1(x>2) | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{5}$=1(x>0) | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1(x>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
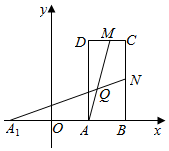 在平面直角坐标系xOy中,四边形ABCD为矩形,A(1,0),B(2,0),C(2,$\sqrt{6}$),又A1(-1,0).点M在直线CD上,点N在直线BC上,且$\overrightarrow{DM}$=λ$\overrightarrow{DC}$,$\overrightarrow{BN}$=λ$\overrightarrow{BC}$(λ∈R).
在平面直角坐标系xOy中,四边形ABCD为矩形,A(1,0),B(2,0),C(2,$\sqrt{6}$),又A1(-1,0).点M在直线CD上,点N在直线BC上,且$\overrightarrow{DM}$=λ$\overrightarrow{DC}$,$\overrightarrow{BN}$=λ$\overrightarrow{BC}$(λ∈R).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{8}{15}$ | C. | $\frac{16}{15}$ | D. | $\frac{8}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com