
已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,lα,lβ,则( )
A.α∥β且l∥α
B.α⊥β且l⊥β
C.α与β相交,且交线垂直于l
D.α与β相交,且交线平行于l
科目:高中数学 来源: 题型:
定点A和B都在平面α内,定点P∉α,PB⊥α,C是α内异于A和B的动点,且PC⊥AC.那么,动点C在平面α内的轨迹是( )
A.一条线段,但要去掉两个点
B.一个圆,但要去掉两个点
C.一个椭圆,但要去掉两个点
D.半圆,但要去掉两个点
查看答案和解析>>
科目:高中数学 来源: 题型:
设m,l是两条不同的直线,α是一个平面,则下列命题正确的是( )
A.若l⊥m,mα,则l⊥α
B.若l⊥α,l∥m,则m⊥α
C.若l∥α,mα,则l∥m
D.若l∥α,m∥α,则l∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,∠BAC=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中,与PC垂直的直线有________;与AP垂直的直线有________.
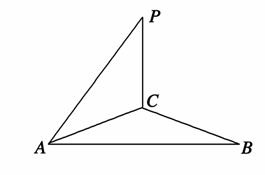
查看答案和解析>>
科目:高中数学 来源: 题型:
对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD;
②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD;
④若AB⊥CD,AC⊥BD,则BC⊥AD.
其中真命题的序号是________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
在平行六面体ABCD-A1B1C1D1中,向量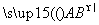 ,
,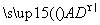 ,
,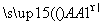 两两的夹角均为60°,且|
两两的夹角均为60°,且|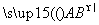 |=1,|
|=1,|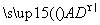 |=2,|
|=2,|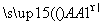 |=3,则|
|=3,则|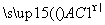 |=( )
|=( )
A.5 B.6
C.4 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com