
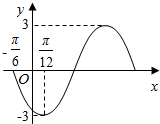
 函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的部分图象如图所示,则其解析式是y=3sin(2x-$\frac{2π}{3}$).
函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的部分图象如图所示,则其解析式是y=3sin(2x-$\frac{2π}{3}$). 分析 由题意求出函数的周期,最大值A,利用函数经过的特殊点,求出ϕ,即可求出函数的解析式.
解答 解:由题意以及函数的图象可知,A=3,T=4×($\frac{π}{12}+\frac{π}{6}$)=π,
所以ω=2,因为函数的图象经过($\frac{π}{12}$,-3),
所以-3=3sin(2×$\frac{π}{12}$+ϕ),|ϕ|<π,所以ϕ=-$\frac{2π}{3}$,
所以函数的解析式为:y=3sin(2x-$\frac{2π}{3}$).
故答案为:y=3sin(2x-$\frac{2π}{3}$).
点评 本题考查函数的解析式的求法,注意函数的图象的特征是解题的关键,考查计算能力.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,$x+\frac{1}{x}>a$成立 | B. | ?x∈R,$x+\frac{1}{x}<a$成立 | C. | ?x∈R,$x+\frac{1}{x}≥a$成立 | D. | ?x∈R,$x+\frac{1}{x}≤a$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com