
为迎接6月6日的“全国爱眼日”,某高中学生会从全体学生中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶),如图,若视力测试结果不低于5.0,则称为“好视力”.

(1)写出这组数据的众数和中位数;
(2)从这16人中随机选取3人,求至少有2人是“好视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记X表示抽到“好视力”学生的人数,求X的分布列及数学期望.
(1)4.75;(2) ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)根据中位数的定义,16个数据按从小到大的顺序排列,第八,九两数的平均数即为这组数据的中位数,16个数据中出现次数最多的两个数,6和7(均为三次)为这组数据的众数;
(2)从这16人中随机选取3人,一共有 基本结果,其中至少有2个是“好视力”的基本结果有
基本结果,其中至少有2个是“好视力”的基本结果有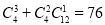 (个),由于是随机选取的,每个基本事件发生的可能性是相等的,于是可利用古典概型的概率公式求解;
(个),由于是随机选取的,每个基本事件发生的可能性是相等的,于是可利用古典概型的概率公式求解;
(3)首选明确X的所以可能取值集合 ,然后求出
,然后求出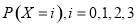 的概率值,从面求得X的分布列及数学期望.
的概率值,从面求得X的分布列及数学期望.
试题解析:【解析】
(1)由题意知众数为4.6和4.7,中位数为4.75.
(2)这是一个古典概型,设至少有2人是“好视力”记为事件A,
则事件A包含的基本事件个数为:
总的基本事件个数为: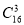
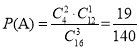
(3)X的可能取值为0,1,2,3.
由于该校人数很多,故X近似服从二项分布B(3, ).
).
P(X=0)=( )3=
)3= ,P(X=1)=
,P(X=1)=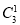 ×
× ×(
×(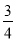 )2=
)2= ,
,
P(X=2)=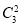 ×(
×(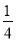 )2×
)2× =
= ,P(X=3)=(
,P(X=3)=(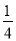 )3=
)3= ,
,
X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故X的数学期望E(X)=3×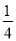 =
=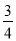 .
.
考点:1、茎叶图及众数、中位数;2、古典概型;3、离散型椭机变量的分布列及数学期望.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:2015届广东省惠州市高三第二次调研考试理科数学试卷(解析版) 题型:选择题
某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数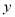 与该班人数
与该班人数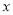 之间的函数关系用取整函数
之间的函数关系用取整函数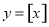 (
(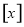 表示不大于
表示不大于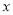 的最大整数)可以表示为( )
的最大整数)可以表示为( )
A.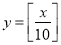 B.
B.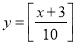 C.
C.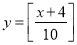 D.
D.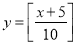
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测理科数学试卷(解析版) 题型:选择题
若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示,
则此几何体的体积等于( )
A. B.
B. C.
C. D.
D.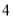
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
给出四个函数,分别满足①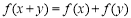 ;②
;②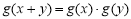 ;③
;③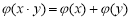 ;④
;④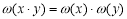 ,又给出四个函数的图象如下:
,又给出四个函数的图象如下:

则正确的配匹方案是( )
A.①—M ②—N ③—P ④—Q
B.①—N ②—P ③—M ④—Q
C.①—P ②—M ③—N ④—Q
D.①—Q ②—M ③—N ④—P
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高三上学期第二次月考理科数学试卷(解析版) 题型:选择题
对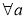 、
、 ,运算“
,运算“ ”、“
”、“ ”定义为:
”定义为: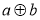 =
=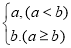 ,
,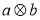 =
=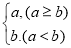 ,则下列各式其中不恒成立的是( )
,则下列各式其中不恒成立的是( )
(1)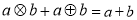 (2)
(2)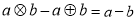
(3)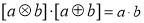 (4)
(4)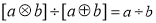
A.(1)、(3)
B.(2)、(4)
C.(1)、(2)、(3)
D.(1)、(2)、(3)、(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com