
分析 设出等差数列的三边为3,3+x,2x+3,由余弦定理列式求出x,则利用余弦定理求出答案.
解答 解:设三角形的三边分别为3,3+x,3+2x,(x>0),
则cos120°=$\frac{{3}^{2}{+(3+x)}^{2}{-(3+2x)}^{2}}{2×3×(3+x)}$=-$\frac{1}{2}$,
化简得:x2+x-6=0,解得x=2或-3(舍去),
∴三角形的3边长分别为:3,5,7.
设最小角为θ,则cosθ=$\frac{{5}^{2}{+7}^{2}{-3}^{2}}{2×5×7}$=$\frac{13}{14}$.
故答案为:$\frac{13}{14}$.
点评 本题考查了等差数列的定义,考查了余弦定理的应用,是基础题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
如图,在三棱柱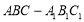 中,
中,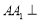 平面
平面 ,
,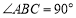 ,
, ,
,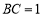 ,
,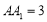 ,
,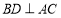 ,
, 为线段
为线段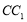 上一点.
上一点.
(Ⅰ)求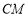 的值,使得
的值,使得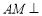 平面
平面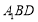 ;
;
(Ⅱ)在(Ⅰ)的条件下,求二面角 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com