
设数列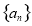 满足:①
满足:①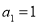 ;②所有项
;②所有项 ;③
;③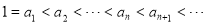 .设集合
.设集合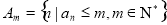 ,将集合
,将集合 中的元素的最大值记为
中的元素的最大值记为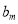 .换句话说,
.换句话说,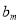 是数列
是数列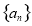 中满足不等式
中满足不等式 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列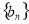 为数列
为数列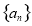 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)请写出数列1,4,7的伴随数列;
(2)设 ,求数列
,求数列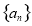 的伴随数列
的伴随数列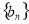 的前
的前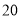 之和;
之和;
(3)若数列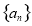 的前
的前 项和
项和 (其中
(其中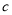 常数),求数列
常数),求数列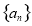 的伴随数列
的伴随数列
的前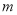 项和
项和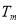 .
.
(1)1,1,1,2,2,2,3;(2)50;(3)
【解析】
试题分析:(1)本题解题的关键是抓住新定义中“ 是数列
是数列 中,满足不等式
中,满足不等式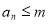 的所有项的项数的最大值”,正确理解题中新定义的内容,根据伴随数列的定义直接写出数列1,4,7的伴随数列;(2)对于这类问题,我们要首先应弄清楚问题的本质,然后根据等差数列、等比数列的性质以及解决数列问题时的常用方法即可解决,根据伴随数列的定义得
的所有项的项数的最大值”,正确理解题中新定义的内容,根据伴随数列的定义直接写出数列1,4,7的伴随数列;(2)对于这类问题,我们要首先应弄清楚问题的本质,然后根据等差数列、等比数列的性质以及解决数列问题时的常用方法即可解决,根据伴随数列的定义得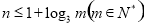 ,由对数的运算对
,由对数的运算对 分类讨论求出伴随数列
分类讨论求出伴随数列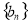 的前20项的和;(3)数列是特殊的函数,以数列为背景是数列的综合问题体现了在知识交汇点上命题的特点,由题意和
的前20项的和;(3)数列是特殊的函数,以数列为背景是数列的综合问题体现了在知识交汇点上命题的特点,由题意和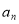 与
与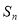 的关系,代入
的关系,代入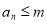 得
得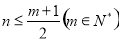 ,求出伴随数列
,求出伴随数列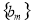 的各项,再对
的各项,再对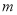 分类讨论得
分类讨论得 .
.
试题解析: 【解析】
(1)由伴随数列的定义得,
数列1,4,7的伴随数列为1,1,1,2,2,2,3(后面加3算对) 5分
(2)由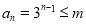 ,得
,得
∴ 当 时,
时, 2分
2分
当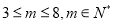 时,
时,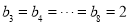 2分
2分
当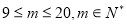 时,
时,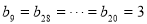 2分
2分
∴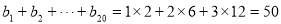 1分
1分
(3)∵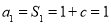 ∴
∴ 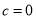 1分
1分
当 时,
时,
∴  1分
1分
由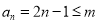 得:
得:
因为使得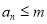 成立的
成立的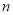 的最大值为
的最大值为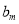 ,
,
所以 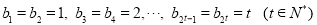 1分
1分
当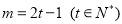 时:
时:
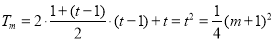 2分
2分
当 时:
时:
 2分
2分
所以 1分
1分
考点:1、新定义求数列;2、数列求和;3、数列的应用.


科目:高中数学 来源:2014-2015学年甘肃省天水市高一上学期期中考试数学试卷(解析版) 题型:选择题
设集合A={x|1<x<4},集合B ={x|-1≤x≤3}, 则A∩(CRB)=( )
A.(1,4) B.(3,4) C.(1,3) D.(1,2)∪(3,4)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
下列说法中正确的是( )
A.事件A,B中至少有一个发生的概率一定比A,B中恰有一个发生的概率大
B.事件A,B同时发生的概率一定比事件A,B恰有一个发生的概率小
C.互斥事件一定是对立事件,对立事件不一定是互斥事件
D.互斥事件不一定是对立事件,对立事件一定是互斥事件
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
两个事件对立是两个事件互斥的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
(2013•宜宾一模)先后抛掷硬币三次,则至少一次正面朝上的概率是( )
A.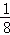 B.
B.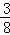 C.
C.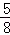 D.
D.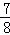
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习文科数学试卷(解析版) 题型:选择题
已知等比数列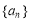 前
前 项和为
项和为 ,则下列一定成立的是
,则下列一定成立的是
A.若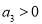 ,则
,则
B.若 ,则
,则
C.若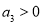 ,则
,则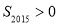
D.若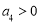 ,则
,则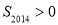
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com