
| P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |

| n(n11n22-n12n21) |
| n1*n2*n*1n*2 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 300 |
| 300+200 |
| 200 |
| 300+200 |
| C | 25 |
| C | 13 |
| C | 12 |
| C | 22 |
| 7 |
| 10 |
| 生产能手 | 非生产能手 | 合计 | |
| 25周岁以上组 | 15 | 45 | 60 |
| 25周岁以下组 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 100×(15×25-15×45)2 |
| 60×40×30×70 |
| 25 |
| 14 |


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源:不详 题型:解答题
| 产量x千件 | 2 | 3 | 5 | 6 |
| 成本y万元 | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.y=-1+x | B.y=1+x | C.y=1.5+0.7x | D.y=1+2x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
| |||||||
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 积极参加班级工作 | 不太积极参加班级工作 | 合计 | |
| 学习积极性高 | 25 | 10 | 35 |
| 学习积极性一般 | 5 | 20 | 25 |
| 总计 | 30 | 30 | 60 |
| P(Χ2≥k0) | 0.05 | 0.025 | 0.01 |
| k0 | 3.84 | 5.02 | 6.64 |
| n(ad-bc)2 |
| (a+c)(b+d)(a+b)(c+d) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①③ | B.②④ | C.①④ | D.都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

 ;
; ;
;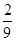 ;
; ;
; .
.| A.2个 | B.3个 | C.4个 | D.5个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com