
分析 (1)利用等比数列的性质列方程解出公比和a2,从而得出通项an;
(2)化简递推式可得$\frac{{b}_{n}}{{b}_{n-1}}$=n,使用累乘法得出通项bn,从而得出{$\frac{{b}_{n}}{{b}_{n+2}}$}的通项,利用裂项法求出Sn.
解答 解:(1)设{an}的公比为q,
则a1a2a3=a23=27,∴a2=3,∴a1=$\frac{3}{q}$,a3=3q,
∵2a2为3a1和a3的等差中项,
∴4a2=3a1+a3,即12=$\frac{9}{q}$+3q,解得q=3或q=1(舍).
∴an=3n-1.
(2)∵bn=bn-1•log3an+1=nbn-1,
∴$\frac{{b}_{n}}{{b}_{n-1}}$=n,又b1=1,
∴bn=$\frac{{b}_{n}}{{b}_{n-1}}$•$\frac{{b}_{n-1}}{{b}_{n-2}}$•$\frac{{b}_{n-2}}{{b}_{n-3}}$•…•$\frac{{b}_{2}}{{b}_{1}}$=n!,
∴$\frac{{b}_{n}}{{b}_{n+2}}$=$\frac{n!}{(n+2)!}$=$\frac{1}{(n+2)(n+1)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,
∴Sn=($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n+1}$-$\frac{1}{n+2}$)=$\frac{1}{2}$-$\frac{1}{n+2}$=$\frac{n}{2(n+2)}$.
点评 本题考查了等比数列的性质,数列求和,属于中档题.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
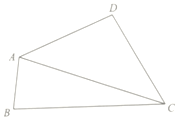 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com